INTRODUCTION

Different from small molecules performing direct glass transition in the fluid states, bulk amorphous linear polymers exhibit unique rubbery states in-between fluid and glassy states in the middle temperature region.^[1] The rubbery states bring nonlinear viscoelasticity as described by empirical KWW equation in the replacement of Debye relaxation, as well as non-Arrhenius fluid behaviors as corrected by the empirical Vogel-Fulcher-Tammann equation in the replacement of Arrhenius equation.^[1] In this sense, the origin of nonlinear viscoelasticity in the rubbery states of bulk amorphous polymers is an important and fundamental issue in polymer physics.

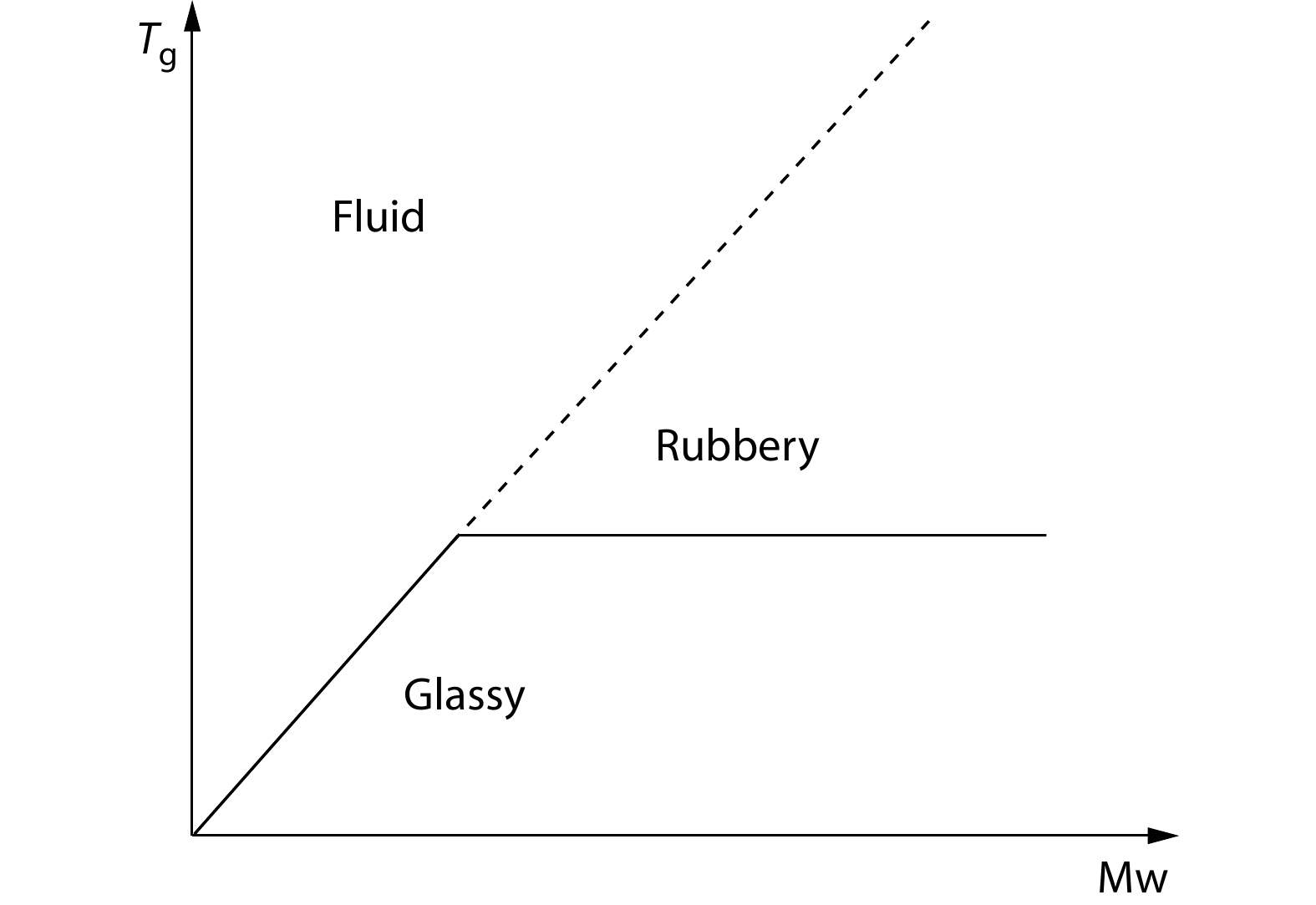
From the viscoelastic point of view, the rubbery states reflect the solid feature of polymers, and the transition from the fluid to the rubbery states appears as a freezing transition from liquid to solid, which typically corresponds to glass transition. In fact, dating back to 1943, Ueberreiter suggested a diagram of glass transition temperatures versus molecular weights to demonstrate a structured liquid above the glassy state of macromolecules but below the extrapolation temperature from the glass transition of small molecules where their glass transition temperatures are still sensitive to molecular weights, as illustrated in Fig. 1.^[2] Frenkel and Baranov proposed the phase dualism theory that macromolecules could have their hierarchical dual transitions from the whole molecules as an entity to their segments as the moving units in the bulk amorphous phase.^[3] Boyer adopted this dualism idea and suggested the substantial liquid-liquid transition of macromolecules above the conventional glass transition temperature of polymer segments, where the intermolecular interactions freeze up macromolecular motions similar to the glass transition of small molecules, although the polydispersity of molecular weights commonly broadens the transition region and thus makes the experimental characterization difficult.^[4] At beginning, the physical cross-linking was assumed for the formation of a transient network.^[5] Later on, upon the prevailing of tube model for long-chain polymer dynamics,^[6] the paradigm shifted to the network of topological entanglements that supposed to entrap macromolecular motions at low temperatures.^[7] However, the tube model was based on an integration of the Rouse model under the conditions of linear viscoelasticity,^[8] and the current hypotheses of chain retraction and convective constraint release on the basis of the tube model were still limited at the mean-field level and the temperature independence for the origin of nonlinear viscoelasticity.^[9,10] The molecular origin of nonlinear viscoelasticity of molten polymers at low temperatures is still unclear.

1Full-screen View

Illustration of Uberreiter’s diagram on glass transition temperatures (T_g) versus molecular weights (Mw), supposing the molecular-weight-sensitive fluid-rubbery transition as an extrapolation from glass transition temperatures of small molecules. Adopted from Ref. [2].

Upon the loading of external stress, the global strain commonly raises the deformation of polymer coils in parallel alignment and uniform orientations (appearing as the experimental optical birefringence^[11]) and their entropy elasticity^[12] resists the external stress as delivered by surrounding intermolecular interactions. Recently, by employing the linear viscoelasticity model of single polymers to expose the intermolecular cooperation in the stress relaxation of bulk amorphous polymers, we performed dynamic Monte Carlo simulations of stress relaxation in parallel-aligned and uniaxially stretched bulk amorphous polymers.^[13] We observed local transient jamming at the transient state that raises an entropic barrier for stress relaxation with linear viscoelasticity in the middle temperature region, and nonlinear deviation occurs in the low temperature region.^[13] The roles of various local chain-unit interactions in the diffusion barrier for stress relaxation with linear viscoelasticity were also investigated.^[14] Hereby, along the same approaches, we continue to investigate how the intermolecular cooperation raises nonlinear viscoelasticity at low temperatures.

SIMULATION DETAILS

Dynamic Monte Carlo simulations of lattice polymers adopted the micro-relaxation modes mimicking real polymers,^[15] which could reproduce the chain-length scaling laws of polymer coil sizes at various concentrations of athermal solutions, as well as the time scaling laws of Rouse dynamics in bulk amorphous 16-mers.^[16] We first prepared the initial state of parallel-aligned and uniaxially stretched bulk amorphous polymers. 1920 polymer chains each holding 128 monomers were preset in the cubic lattice space X*Y*Z= 16*128*128 sites, and the remaining non-occupied sites were served as free volume for polymer micro-relaxation. Under athermal conditions except for two chain ends of each polymer separately restricted at two boundary planes along X-axis, they were relaxed into bulk amorphous states. Double occupation and bond crossing were avoided during polymer micro-relaxation. After that, with two chain ends restricted at X-axis borders, all the polymers were stretched step-by-step along X-axis up to 100% strain. The details of each-step homogeneous stretching for one lattice could be found from our previous simulations of strain-induced polymer crystallization.^[17] Then with the global strain self-maintained at 100%, the restrictions of two chain ends were released, and the internal tensions of the polymers were relaxed^[13] from the initial modulus M₀ in sequential time segments by following the time evolution of Brownian motions of each coil mass center according to the Maxwell model of linear viscoelasticity^[18] for Debye relaxation.^[19] In each segment t (here 200 Monte Carlo (MC) cycles, while the time unit of MC cycle was defined as once trial move of each monomer on average), the residual modulus of each polymer was decaying with the square displacement of coil mass center, as given by

1 $M \left(t\right)={M}_{0}{\rm{exp}}\left\{-\frac{{[r \left(t\right)-r(0 \left)\right]}^{2}}{{{R}_{\rm{g}}}^{2}}\right\}$

where the Debye relaxation time t was replaced by the mean-square displacement of coil mass centers at the coordinate r according to Einstein’s theory of Brownian motions,^[20] the characteristic time was correspondingly replaced by the square radius of gyration R_g² at the beginning of each time segment, and M₀ was updated with the residual modulus of the last time segment. Although each polymer was assumed to follow Debye relaxation in each time segment, its relaxation behavior would be sensitive to the intermolecular cooperation for local Brownian motions. In this sense, our simulations reflected the mechanism of intermolecular cooperation in the stress relaxation process of bulk amorphous polymers. We then employed the conventional Metropolis sampling algorithm^[21] with the total potential change of micro-relaxation, as given by

2 $\frac{\Delta E}{kT}=\frac{\sum x\times M}{{M}_{0}}\times \frac{{M}_{0}}{kT}$

where Σx was summed over the monomer distances away from the coil mass center for those monomers involved in each step of micro-relaxation (x would be negative if the monomer left away from the mass center along X-axis on either side of two, reflecting the internal tension in balance with the restoring force of entropy elasticity), T was the temperature, and k was Boltzmann’s constant. The reduced temperature was kT/M₀. Finally, we only considered those polymers in the central bulk phase and did not count those polymers nearby the lateral free-standing surfaces.^[13] Three repeating simulations were performed under parallel conditions for total 2340 bulk amorphous polymers to be calculated in the following results.

RESULTS AND DISCUSSION

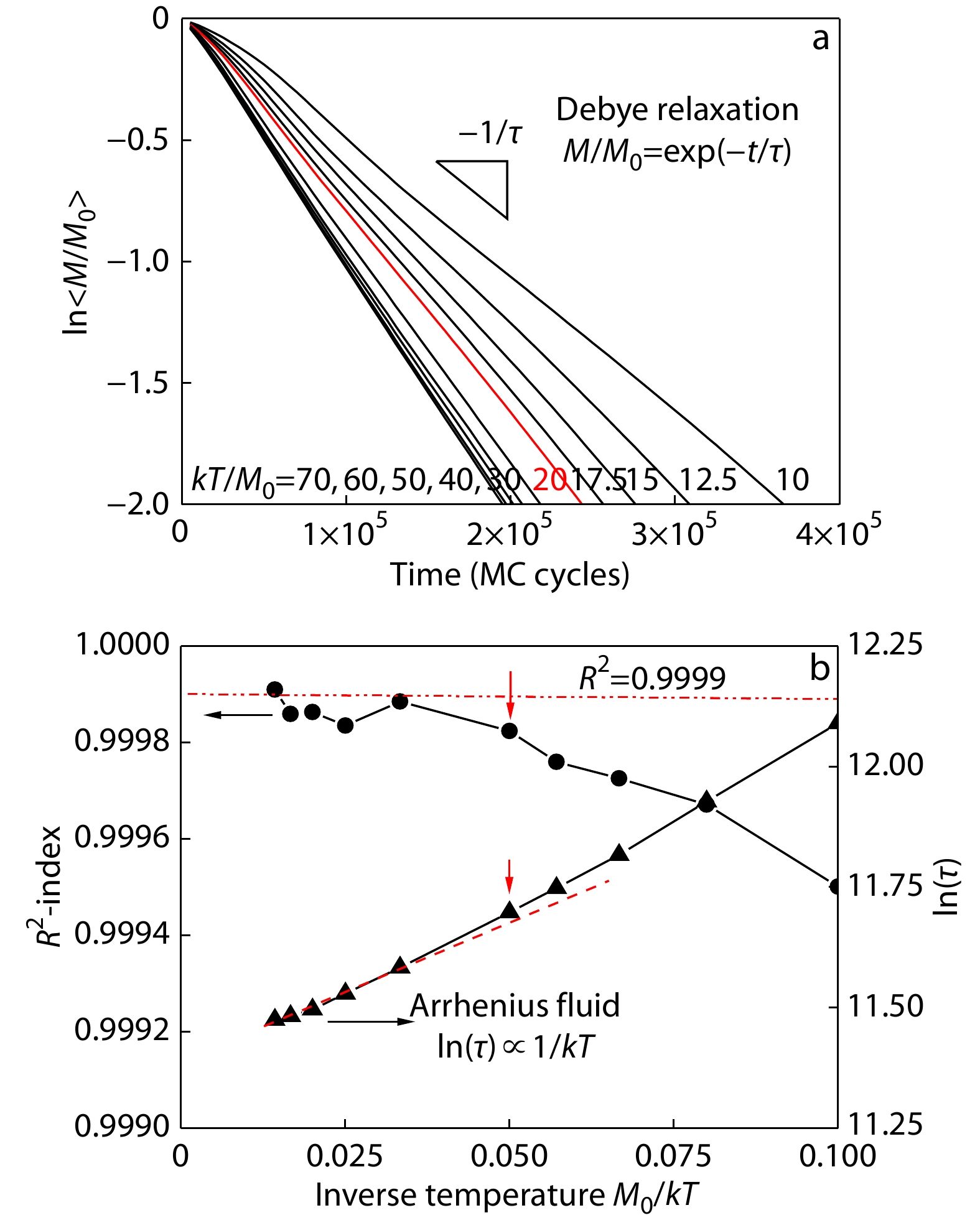
We first made the Debye relaxation analysis on the time evolutions of the residual moduli averaged over all the bulk polymers at the various temperatures from kT/M₀=70 to 10, as the results shown in Fig. 2(a). One can see that above the temperature 20, the relaxation curves follow well the Debye relaxation behaviors, while below 20 the stress relaxation process is retarded, in particular at the early stages. If we made linear regression on the relaxation curves, their relevant R-square indexes indicated the deviation from the standard criteria 0.9999 below the temperature 20, as shown in Fig. 2(b). The deviation from Debye relaxation implies nonlinear viscoelasticity at low temperatures. Meanwhile, the slopes of linear regression give their characteristic time, which follow well the Arrhenius fluid behaviors^[22] above the temperature 20. The deviation from Arrhenius fluid behaviors also demonstrates nonlinear viscoelasticity in the low temperature region.

2Full-screen View

(a) Time evolution of residual moduli ln<M/M₀> averaged over all the polymers within temperature window from 10 to 70 as labeled in the same sequences. The Debye relaxation curves give the characteristic time τ on their slopes. The red curve highlights the demarcation of stress relaxation behaviors at temperature 20. (b) Relevant R²-indexes (left axis) and Arrhenius plot of characteristic time (right axis) obtained from linear regression on the Debye relaxation curves in (a) at various temperatures. The red arrows indicate both the deviations from the standard level of R²=0.9999 and from Arrhenius fluid behaviors starting at temperature 20.

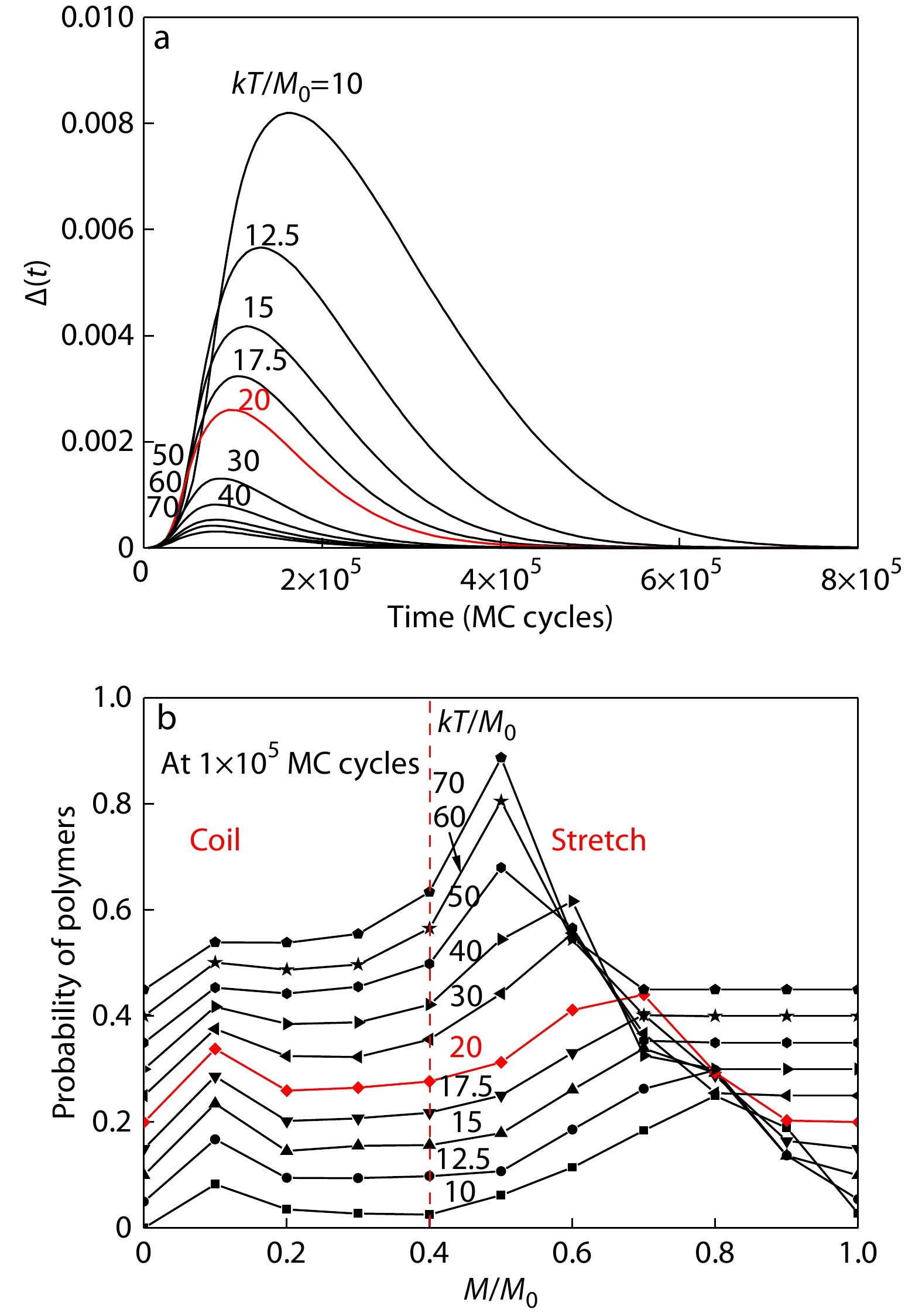
In previous simulations,^[13] we made the fluctuation analysis on the residual moduli among polymers under the linear response condition. Here, we continued to observe the fluctuation of the residual moduli among polymers as the time-dependent autocorrelation function^[23] defined by

3

where the average <…> was calculated over all the counted bulk polymers. The time-dependent autocorrelation functions of the residual moduli among bulk amorphous polymers at various temperatures are summarized in Fig. 3(a). One can see that, in the high temperature region showing linear viscoelasticity, the fluctuations peaks are stable with the transient peak periods nearby 1×10⁵ MC cycles. In contrast, in the low temperature region since 20, the fluctuation peaks become significantly higher and even shift to longer transient periods, indicating significant retardation behaviors in the early stage of stress relaxation. In our previous simulations,^[13] we took 1×10⁵ MC cycles as the transient periods to observe the distributions of residual moduli among polymers, and we found the coexisting of stretch and coil states of polymers with the demarcation of residual moduli 0.4. Fig. 3(b) clearly demonstrates the bistable states of stretches and coils among bulk polymers at the periods of 1×10⁵ MC cycles during stress relaxation even below the temperature 20. One can see that stretch polymers become more stretched in the low temperature region, and some polymers appear as even no relaxation (M/M₀=1), indicating their frozen-up at this early stage of stress relaxation.

3Full-screen View

(a) Time evolution curves of thermal fluctuation Δ(t) of residual moduli M/kT among bulk polymers at various temperatures as labeled. The red curve indicates the demarcation behaviors at temperature 20. (b) Distribution of residual moduli among bulk polymers at the time period of 1×10⁵ MC cycles upon stress relaxation at various temperatures as labeled. The curves are shifted up with equal spacing at zero modulus for clarity. The dashed vertical line indicates the demarcation between the stretch fraction and the coil fraction of bulk polymers.

One of advantages of our modelling is that a few athermal single vacancy sites play the role of free volume in the micro-relaxation of bulk amorphous polymers. The vacancy sites of free volume reflect the local mobility of polymers in the stress relaxation process. Therefore, we calculated the distributions of single vacancy sites along X-, Y- and Z-axes at the same periods of 1×10⁵ MC cycles upon stress relaxation at various temperatures. We found that the vacancy sites are homogeneously distributed on the Y-Z plane, but heterogeneously distributed along X-axis at various temperatures as the results summarized in Fig. 4. The most important observation is that, above the temperature 20, the vacancy sites are distributed only slightly more around the central area along X-axis due to the richness of coil polymers there, but in the low temperatures since 20, the vacancy sites are significantly concentrated in the central area, leaving almost no vacancy sites nearby two stretching ends of polymers along X-axis. The situation of no vacancy site implies global jamming along the Y-Z planes nearby two stretching ends of polymers. At low temperatures, the tentative frozen-up of two stretching ends of polymers will play the role of physical cross-linking to make dominantly elastic response of the solid at the early stage of stress relaxation, corresponding to the rubbery states of bulk amorphous polymers.

4Full-screen View

Distributions of single vacancy sites along X-axis at the period 1×10⁵ MC cycles of stress relaxation at various temperatures from 10 to 70 as labeled besides the curves. The red curve at the temperature 20 indicates the demarcation between linear and nonlinear viscoelasticity regions.

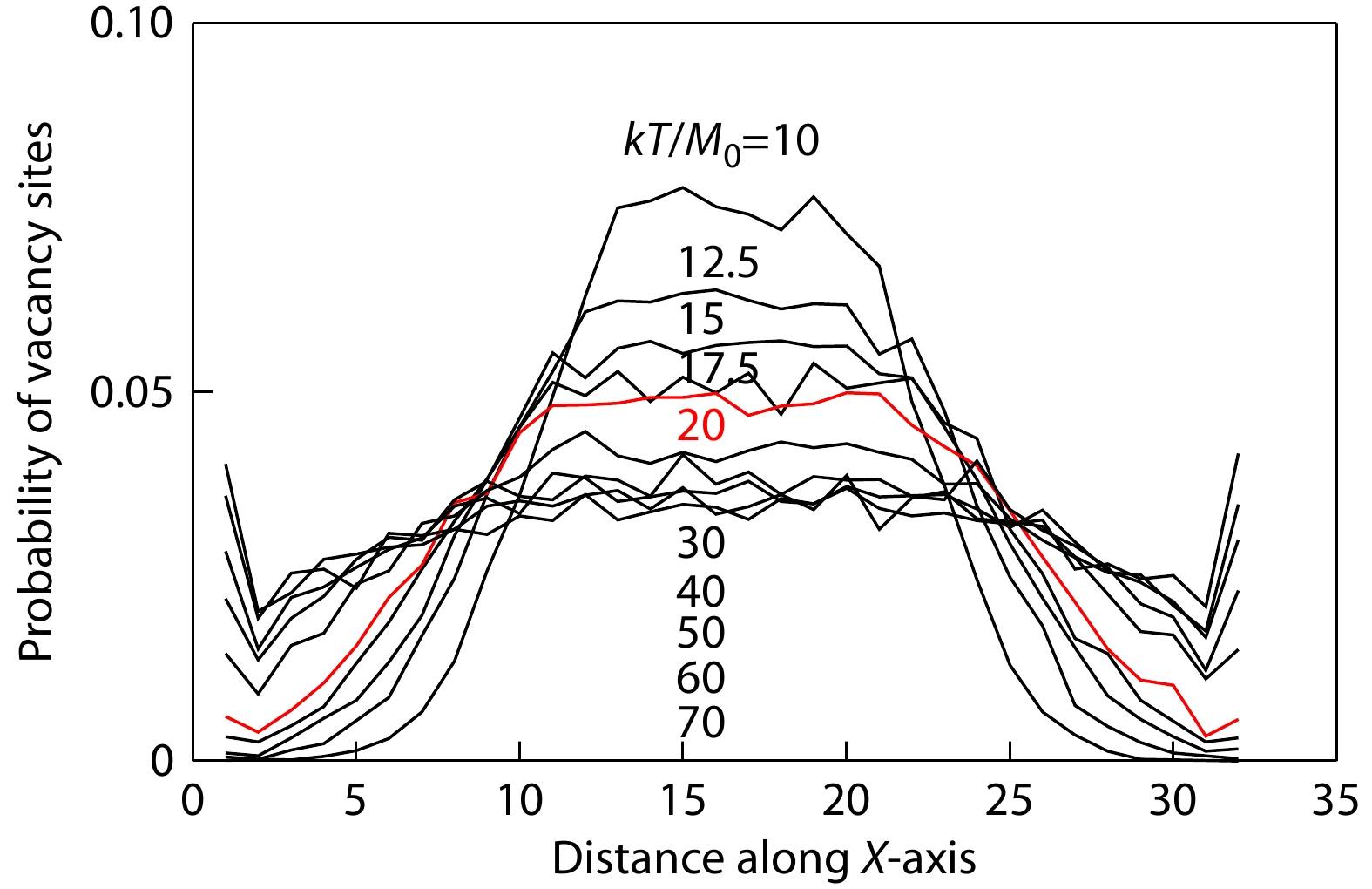
According to the equation of state of the rubber,^[1] the modulus of the conformational entropy elasticity decreases with temperatures. Thus, the entropy elasticity of bulk amorphous polymers will eventually lose its competition to the external loading stress below a critical temperature. Since the modulus of polymer entropy elasticity becomes lower than the residual modulus at low temperatures, the relaxation time of polymers is longer than what the initial modulus M₀ expects to relax, corresponding to the situation as described by Deborah number larger than one. Deborah number was traditionally defined by the ratio of relaxation time to observation time.^[24] In this situation, the first response of the conformational change in single polymers to the relatively stronger stress will be further stretching rather than immediate retraction under a constant global strain. In consequence, the monomers are tentatively overcrowding at two stretching ends of polymers, and the global jamming along the two Y-Z planes nearby two stretching ends retards the stress relaxation of single polymers at the early stage before reaching their transient states. Therefore, the transient states of stress relaxation are delayed into longer periods at low temperatures, as shown in Fig. 3(a). The extra-slowing down at the early stage results in nonlinear deviations from Debye relaxation and Arrhenius fluid behaviors, as shown in Fig. 2(b). Fig. 5 illustrates two snapshots of free volume distributions for the contrast situations of linear and nonlinear viscoelasticity at the early stages of stress relaxation separately at high and low temperatures. The depletion of free volume nearby two polymer ends at low temperatures tentatively retards the early stage of stress relaxation, resulting in the rubbery states of bulk amorphous polymers.

5Full-screen View

Snapshots of bulk amorphous polymers at the periods of 1×10⁵ MC cycles for stress relaxation separately at the high temperature of 50 and at the low temperature of 10. Polymer bonds are drawn as blue cylinders, and single vacancy sites of free volume are drawn as white spheres. The free volume is depleted nearby two stretching ends of polymers at low temperatures.

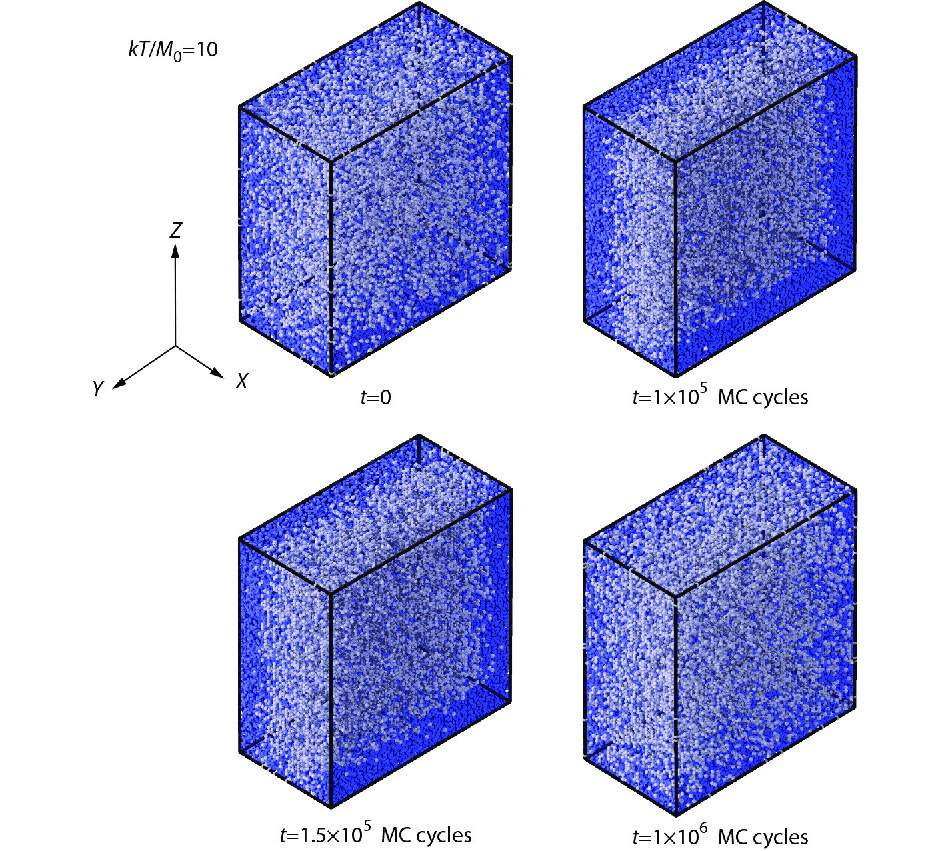
During the stress relaxation process at the low temperature 10, the early-stage global jamming states nearby the stretching ends of polymers at the period 1×10⁵ MC cycles could be sustained to the transient period 1.5×10⁵ MC cycles, showing the free volume distributions apparently different from the initial and the end states, as shown in Fig. 6.

6Full-screen View

Snapshots of bulk amorphous polymers at the sequential periods of 0, 1×10⁵, 1.5×10⁵ and 1×10⁶ MC cycles of stress relaxation at the low temperature 10 (See Fig. 3a). Polymer bonds are drawn as blue cylinders, and single vacancy sites of free volume are drawn as white spheres. The free volume is depleted nearby two stretching ends of polymers at the early stage (1×10⁵ MC cycles) and the transient stage (1.5×10⁵ MC cycles).

CONCLUSIONS

In the present simulations, we extended our previous simulations into the low temperature region, where stress relaxation exhibits an extra-slowing down deviated from the linear viscoelasticity region where Debye relaxation and Arrhenius fluid behaviors could be reproduced. We performed fluctuation analysis and structural analysis on the residual moduli among polymers in the stress relaxation process at various temperatures. We observed the early-stage retardation of stress relaxation raised by tentative global jamming nearby two stretching ends of polymers at low temperatures, which demonstrated the mechanism of intermolecular cooperation as the origin of nonlinear viscoelasticity of bulk amorphous polymer as well as their rubbery states.

Our results suggested the scenario that, since the modulus of polymer entropy elasticity decreases with temperature and eventually loses its competition to the external loading stress, as described by Deborah number larger than one, thus under constant global strain polymers intend to perform further stretching at the first moment of stress relaxation, which enables their monomers to be overcrowding nearby two stretching ends; in consequence, the tentative global jamming along the planes normal to the stretching direction plays the role of physical cross-linking at two stretching ends of polymers in the early-stage retardation of stress relaxation before reaching their transient states. Such frozen-up of polymers at low temperatures is responsible for the occurrence of nonlinear viscoelasticity and rubbery states in bulk amorphous polymers. If we follow Uberreiter’s idea on the extrapolation of glass transition from low molecular weight to high molecular weight, the intermolecular cooperation mechanism of polymer fluid-rubbery transition brings new insights into the intermolecular cooperation nature of glass transition of small molecules. In our present simulations, we considered only the temperature factor for nonlinear viscoelasticity of polymers, we will further consider the strain factor as well as the chain-length factor, and we will also investigate how chain-unit interactions play their roles in the fluid-rubbery transition of bulk amorphous polymers.