INTRODUCTION

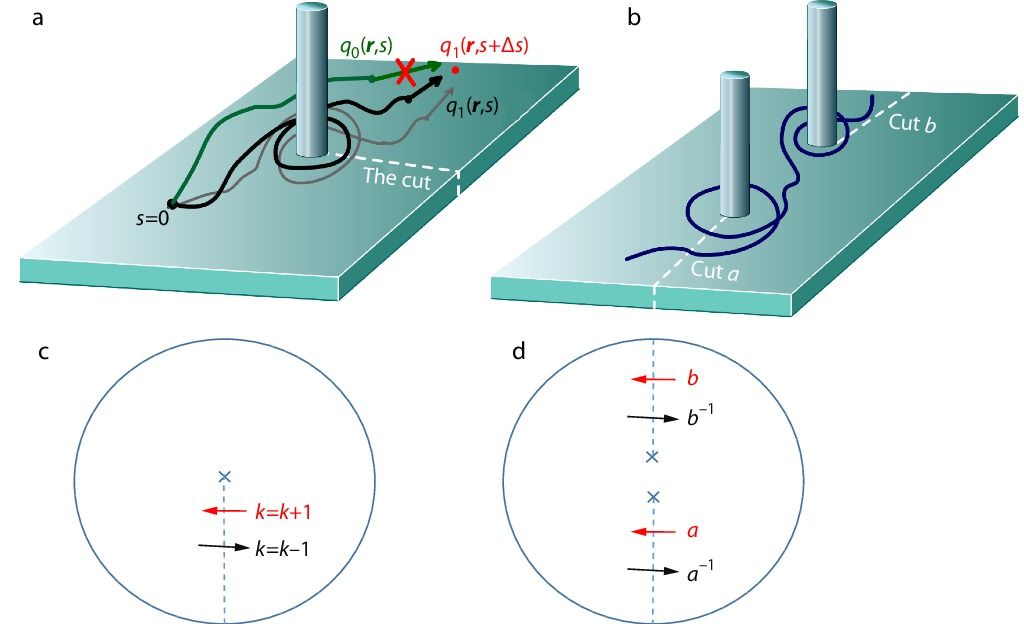
Polymer entanglement presents a great challenge in polymer physics. The development of a theoretical framework for the study of dynamic topological constraints is an extremely difficult and unsolved problem. On the other hand, great progresses have been made for the less difficult problem involving polymers entangled with static topological constraints. For the case of one polymer chain entangled with one static topological constraint, pioneering work has been carried out by a number of researchers.^[1−8] In particular, using an analogue with the Schrödinger equation, Edwards^[2,3] was able to derive the two-segment correlation function of a polymer chain winding around a pole with a given winding number on a 2D plane (Fig. 1a). It was speculated that this method could be extended to the cases of a polymer chain entangled with more than one poles or multiple static topological constraints. However, the problem of one polymer chain under multiple static topological constraints remains unsolved^[7] because of the noncommutative character of multiple entanglements.^[8]

1Full-screen View

A new strategy to solve the problem of polymers entangled with static topological constraints. (a) A polymer chain entangled with one pole. The propagator q₀(r, s) cannot diffuse into q₁(r, s + Δs) because entangling modes are different for these two quantities. In (c), the subspaces labelled with k =$\cdots -1, 0, 1 \cdots$. Crossing the cut from the right to left the winding number k will get a`+1'. In (b) and (d), a polymer is entangling with two poles. For each pole, one can define a cut that connects the pole to an infinity point. The generator a corresponds to cross the cut a from the right to left while its inverse a⁻¹ from left to right. The entangling mode of (b) corresponds to b⁻¹ a⁻².

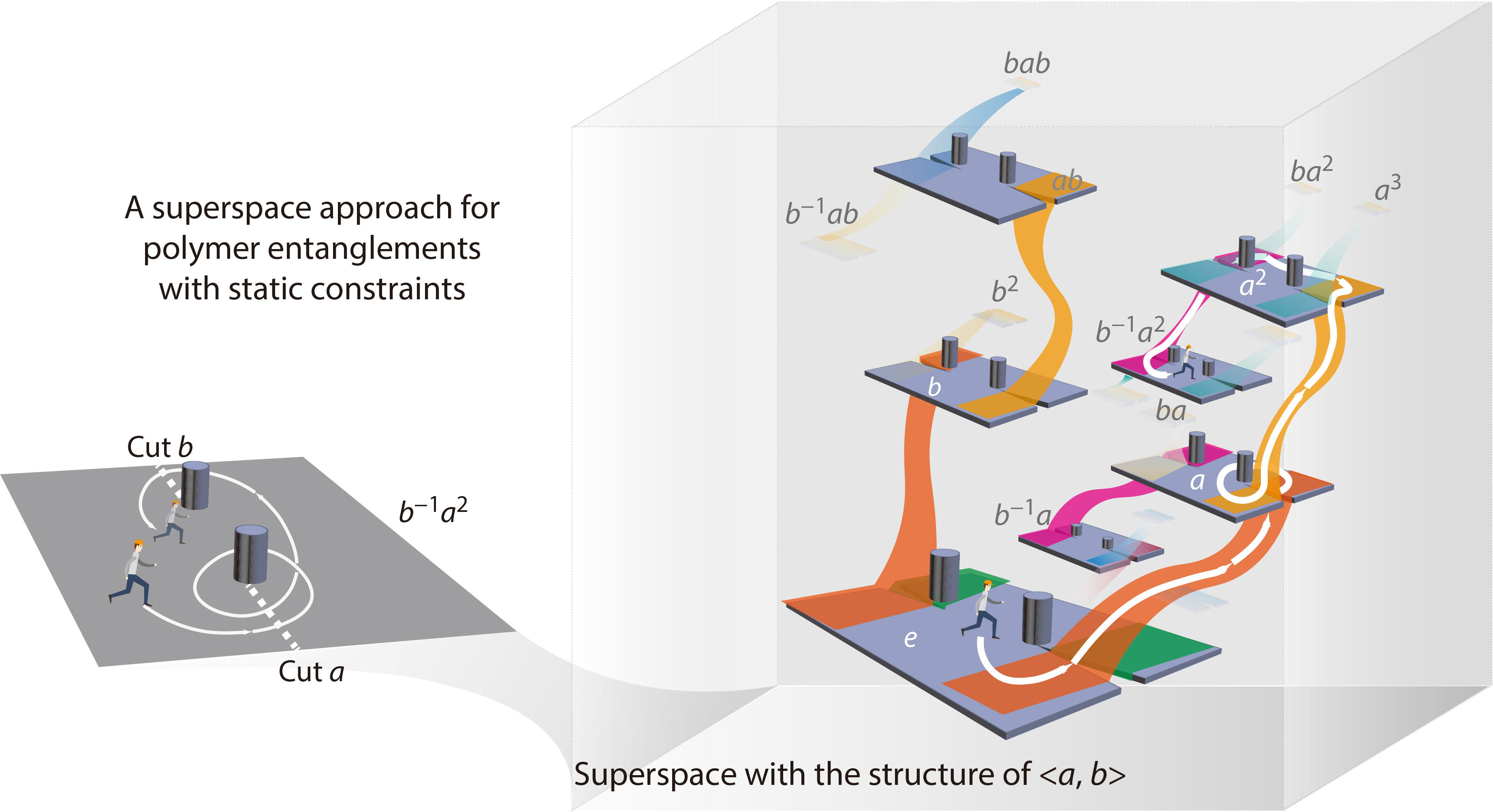
In the current study, we formulate the topological constraints of an entangled polymer chain using a superspace-based field theoretical approach, which combines the method from random walks on free groups^[9] and Edwards' approach^[2] for the one-pole case. In this theoretical formulation, the probability distribution of the chain segments is obtained by solving the Fokker-Planck or diffusion equation in a superspace consisting of a set of subspaces, and each subspace corresponds to a given entangling mode. This new approach is applied to the problem of a polymer chain subjected to n poles on a 2D plane. In this case, the superspace has a mathematical structure isomorphic to the n-generator free group.^[10] For the case with one entangling pole, the superspace approach gives a simpler solution as compared with the previous approaches.^[1−6] Furthermore, the force-extension curve of a polymer chain entangled with two poles is calculated, which contains a term originated from the topological constraints. The topological term of the force-extension curve is determined by a topological charge number which is an invariant for a given polymer entangling mode but it does not solely depend on the winding number. Physically, the topological charge reflects the number of independent perturbations along the entangled chain that is not Gaussian^[11] or it measures how much the chain conformation deviates from Gaussian due to the topological constraints. To our best knowledge, this topological invariant is a new type of topological charge and is unique for Gaussian chains since there is no such correspondence in other fields ^[12] where the topological invariants normally depend on the winding number.

THEORETICAL METHOD

The theoretical approach starts with the partition function of an ideal polymer chain whose conformation is described by a space curve ${\boldsymbol{R}}\left(s\right)$,^[2,13,14]

1

where the pre-factor in the exponential is $N{b}^{2}$ instead of $3N{b}^{2}/2$ because the chain is confined in a plane. In practice, this path integration is computed in terms of the end-integrated distribution function or propagator, $q({\boldsymbol{r}},s)$, of the polymer according to ${\cal{Z}}=\int q({\boldsymbol{r}},s=1){\rm d}{\boldsymbol{r}}$. The propagator is in turn defined as the end-integrated probability distribution of the $s$^th segment,

2

The propagator $q({\boldsymbol{r}},s)$ could be regarded as the correlation function between the initial segment and the segment $s$. Instead of performing the path integration, the function $q({\boldsymbol{r}},s)$ can be obtained as the solution of the Fokker-Planck or diffusion equation:^[2,13,14]

$\frac{\partial q}{\partial s}=\frac{N{b}^{2}}{4}{\nabla }^{2}q$

For an ideal chain in the presence of topological poles, this correlation function not only depends on the arclength $s$ and the position r but also depends on the “history” or the trajectory of the chains (Fig. 1a). For example, if ${q}_{1}$ denotes $q$ that winds the pole once and ${q}_{0}$ does not wind the pole, then ${q}_{0}$ cannot "diffuse" into ${q}_{1}(s+\Delta s)$. While in the conventional field theory of Gaussian chain, the propagator does not specify the entangled mode so ${q}_{0}$ can "diffuse" into ${q}_{1}(s+\Delta s)$, which is obviously not realistic for a real entangled polymer chain. As a consequence of this topological constraint, special techniques are required to treat the multi-valued nature of the problem.

One method to explicitly incorporate the topological constraints of the poles into the probability distribution of the polymer conformations is to express the end-integrated propagator $q({\boldsymbol{r}},s)$ in terms of entangling modes ${q}_{\rm{g}}({\boldsymbol{r}},s)$, where the subscript g denotes different entangling modes of the chain section $0\to s$ relative to the n-poles. Each mode ${q}_{\rm{g}}({\boldsymbol{r}},s)$ lives in its own two-dimensional subspace labeled by g and, specifically, ${q}_{\rm{g}}({\boldsymbol{r}},s)$ is the solution of the diffusion equation within that subspace,

3

RESULTS AND DISCUSSION

From the perspective of group theory, the index g can be regarded as an element of the n-generator free group ${G}_{n}$,^[10] which could be properly defined using a group-acting-on-a-set method:

1. A superspace is defined as a set containing all the subspaces ${\mathbb{S}}_{n}=\left\{{S}_{\rm{g}}\right\}$ that represent all possible entangling modes due to the n poles.

2. There are n basic operations or generators $\{a,b,c\dots \}$, each corresponding to crossing a cut of a pole in some given direction (see Fig. 1). The action of the generator on the subspaces obeys the rule $a{S}_{\rm{g}}={S}_{\rm{ag}}$. In general, these generators do not commute.

3. The n-generator free group ${G}_{n}= <a,b,c,\dots >$ can be constructed based on these n generators. There is a one-to-one mapping from the superspace to the group ${G}_{n}$, i.e., $\mathbb{S}=\left\{{S}_{\rm{g}}\right|g\in {G}_{n}\}$.

Operationally, ${G}_{n}$ reflects how the subspaces are glued together at the cuts to form the superspace. In practice, it specifies the boundary conditions of the propagator at the cuts. Details are given in the electronic supplementary information (ESI). In order to study the statistical mechanics of a polymer chain subjected to the poles, the entangling modes of the chain relative to the poles need to be specified. Mathematically, an entangling mode is uniquely specified by putting one end of the chain on a subspace ${S}_{0}$ and the other end on another subspace $g{S}_{0}$ with $g\in {G}_{n}$. The group element $g$ uniquely determines the entangling mode. In what follows we apply this superspace approach to the one-pole and two-pole problems, focusing on computing the corresponding force-extension curves of the chain.

For the one-pole problem, the superspace is the complex logarithm Riemann surface (CLRS) (Fig. S1 in ESI). The 1-generator free group is simply isomorphic to the whole-number group or the one-winding-number representation $k=\{\cdots -{1,0},1\cdots \}$. Obviously, all the elements in this group commute. In this case, the problem can be analytically solved (see ESI). Furthermore, numerical solutions of the diffusion equation have also been obtained using nine subspaces with $\left|k\right|\le 4$.^[15] Compared with previous work,^[1−6] the superspace approach gives a simpler solution to the one-pole problem (Eqs. S1−S5 in ESI).

For the two-pole problem, the superspace corresponds to the case with n=2, where ${G}_{2}=<a,b>$ is the two-generator free group. Because the two generators, $a$ and $b$, do not commute, the group element or the 'word' normally takes the form of, e.g., ${a}^{2}{b}^{-2}{a}^{-1}b(\ne a{b}^{-1})$. Therefore, the group cannot be represented by two winding numbers $({k}_{\rm{a}},{k}_{\rm{b}})$ nor by two phase angles ${e}^{i{\psi }_{\rm{a}}+i{\psi }_{\rm{b}}}$. Analytic solutions of the two-pole problem are not available. Instead we numerically solve the problem with two poles. Specifically, the diffusion equation is numerically solved using 53 subspaces with the total winding number smaller than 4, i.e., $\left|{k}_{\rm a}\right|+\left|{k}_{\rm b}\right|<4$. The Cayley graph of these 53 subspaces is shown in Fig. 2, demonstrating how these subspaces are glued together and also specifying the intricate boundary conditions of the diffusion equation (details are given in ESI). We also have carried out detailed calculations to confirm that these 53 subspaces are sufficient for the numerical computations (Fig. S3 in ESI).

2Full-screen View

A Cayley graph for the two-generator free group ${G}_{2}$ of the two-pole case. Only 53 group elements or subspaces with the total winding number smaller than 4 ($\left|{k}_{\rm a}\right|+\left|{k}_{\rm b}\right|<4$) are given. The meanings of the group generators of $a$ and $b$ in terms of topological constraints are shown in the center of the graph. Each group element represents a specific entangling mode.

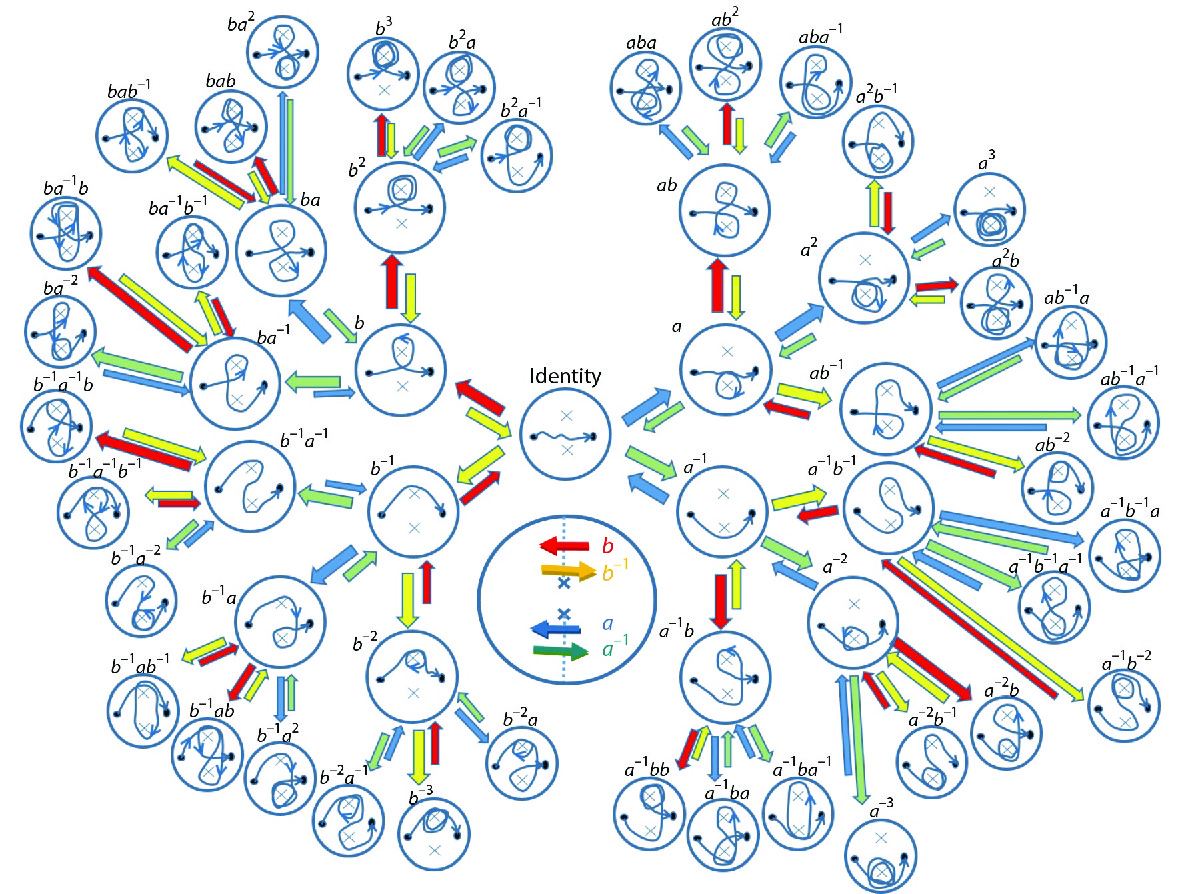
We emphasize that a polymer chain entangled with multiple poles can be seen as a random walk on a superspace $\left\{{S}_{\rm{g}}\right\}$ with a free group structure, which is different from the random walk on free groups^[9] where the continuous space has been actually neglected (or they only discuss the probability function of ${q}_{\rm{g}}$ which does not depend on the position r). In the random walk on free groups,^[9] they 'jump' between the group elements of a given free group; while in this work, we 'walk' in the subspaces $\left\{{S}_{\rm{g}}\right\}$.

In order to obtain basic statistical properties of a polymer chain subjected to static topological constraints, the force-extension curves of a polymer entangling with one pole or two poles in a 2D plane are computed. The procedure of calculating the force-extension curves is illustrated by the one-pole problem. In this case, we let the polymer wind the pole k-times with corresponding winding number k or −k and fix the two ends with a distance L between them. We then numerically or analytically solve the diffusion equation of $q$, which in turn gives the partition function ${\cal{Z}}\left(L\right)$ and the corresponding free energy, $G\left(L\right)=-{k}_{\rm{B}}T{\rm {In}}{\cal{Z}}\left(L\right)$. The force can finally be calculated using $F\left(L\right)=-\partial G/\partial L$.

Fig. 3 shows the force-extension curves of several entangling modes of a polymer chain in the presence of one pole or two poles, along with some of the chain density patterns. From the force-extension curves, it can be seen that when the extension L is small, the force does not exhibit a linear dependence on the extension. This non-linearity could be qualitatively explained by an entropy-loss argument (see Fig. S5b in ESI).

3Full-screen View

(a) Force-extension curves of different winding numbers for the one-pole case. The extension L measures the distance between the two chain ends. The square is given by the numerical calculations. Solid line is obtained by analytically solving the diffusion equation on a complex Riemann plane (Eq. S3 in ESI). Dash line is given by the blob model with perturbations. (b) Force curves of different entangling modes for the straight case of the two-pole problem (Chain ends and poles are in a straight line). Solid line is by numerical calculations and dash line by a blob model with perturbations. (c) Force curves of different entangling modes for the vertical case of the two-pole (Chain ends and poles are vertical). (d) Patterns of chain segment density for different entangling modes in (b) and (c). Upper ones are for (b) while lower ones for (c). Parameter setting: chain length $N=400$, pole radius ${r}_{\rm{p}}=\sqrt{2}b$ and the distance between poles $d$ is $5b$ with $b$ the Kuhn length.

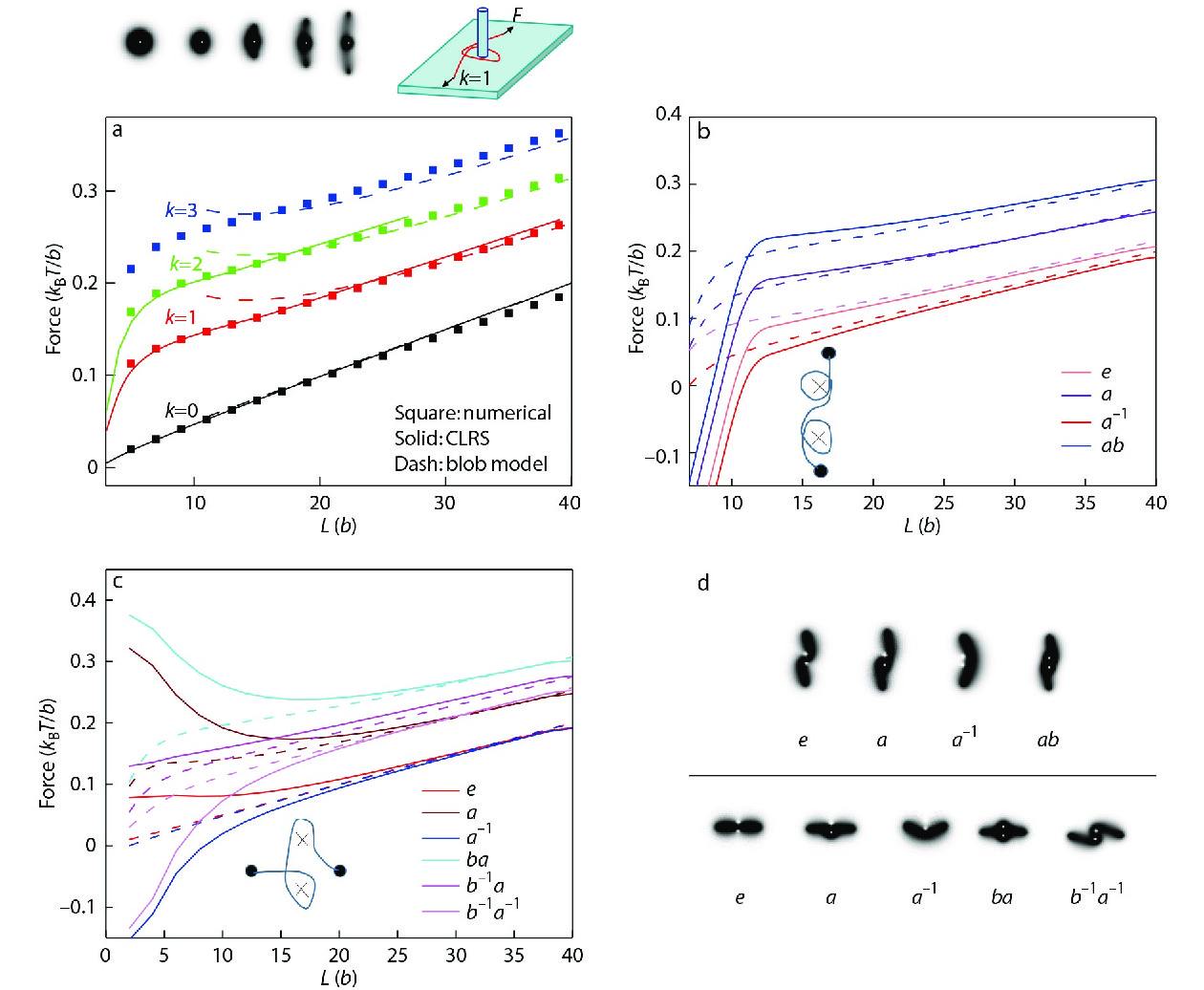
For large extensions, the force-extension curves exhibit a linear behavior with gaps between different entangling modes. These force gaps could be well explained by a blob model^[16] with small perturbations (see ESI). Specifically the blob model predicts that the force-extension curves at large extension L could be approximated by,

4

where $l(L,{r}_{\rm{p}},d)$ is an effective extension of the polymer chain, which is a function of the extension, the pole radius ${r}_{\rm{p}}$ and poles' configuration characterized by the poles' separation d in the two-pole case. The quantity Z is a topological charge number of the entangling mode. For one-pole case, Z=0 for k=0 and Z=1 otherwise. For two-pole case, the dependence of Z on the entangling modes are listed in Fig. S7 (in ESI).

The first term in Eq. (4) is a linear function of the effective extension l, which describes an entropic spring with an extension l. Obviously this term depends on the specific entangling mode (including the winding number) as well as on the pole configuration. For example, in the one-pole case $l\left(L,{r}_{\rm{p}},d\right)\approx L+2k{\text{π}}{r}_{\rm{p}}$, where the contribution $2k{\text{π}}{r}_{\rm{p}}$ (k is the winding number) presents a hidden extension. The expressions of l for several entangling modes of the two-pole case are given in ESI. It is noted that Eq. (4) is only valid if there is no knot or self-entanglement inside the polymer chain. Knots inside the chain will certainly increase the hidden extension by a small amount for a real polymer.

The distance d between the topological constraints is also important for the entangled behavior of polymers, as pointed out in previous literature.^[17,18] In this work, we found the distance d mainly influences the force through the hidden extension l(L, d) as shown in Sect. IV-2 in ESI. Specifically, for $L\gg d\gg {r}_{\rm{p}}$ and the entangled mode that can be expressed as ${a}^{{n}_{1}}{b}^{{n}_{2}}{a}^{{n}_{3}}\dots {b}^{{n}_{m}}$ with $\left\{{n}_{\rm{k}}\right\}$ non-zero integers, the hidden extension is elongated by about $\left(m-1\right)d$ for the straight case and by about $\left(m-1\right)d+{d}^{2}/L$ for the vertical case.

The second term in Eq. (4), which is proportional to $1/l$, can be identified as a pure topological term which depends on the topological charge number Z. This term is universal and it reveals the fundamental properties of the static topological constraints of polymer entanglements. In particular, the topological charge number depends on the specific entangling mode but, interestingly, it is independent of the winding number. This independence of the winding number is demonstrated in Fig. S2 (in ESI). Furthermore, we have analytically shown that for the one-pole case with ${r}_{\rm{p}}=0$, $F=2l{k}_{\rm{B}}T/N{b}^{2}+{k}_{\rm{B}}T/l+O\left({(1/l)}^{2}\right)$ when ${l}^{2}\gg N{b}^{2}$ (see Eq. S15 in ESI), firmly confirming the existence of the topological charge for an entangled polymer with a single static topological constraint. The existence of the topological charge(s) can be further confirmed by the comparison of the force curves given by the numerical calculations and those by the blob mode (Eq. 4).

Although the topological charge emerges analytically in the one-pole case (Eq. S15 in ESI), the physics behind this topological invariant is obscured by the tedious mathematical derivations. We have discovered that the topological charge could be extracted from an entangled chain by perturbing the blob model. Intuitively, if one perturbs an unentangled Gaussian chain (Fig. 4a) with a displacement of the order of ${\Delta }x$, the chain will be elongated by an amount of the order of ${\Delta }{x}$². Such second-order terms could be eliminated by the Gaussian integral when all possible small perturbations are summed up to obtain the partition function (a rigorous analysis is given in ESI). Therefore, perturbing an unentangled Gaussian chain will not result in any topological charges. This type of perturbations will be termed as the Gaussian perturbation. If the chain is winding a pole once, a perturbation ${\Delta }x$ (Fig. 4b) will cause the chain to elongate by an amount of the order of ${\Delta }x$, which cannot be absorbed by the Gaussian integral. Instead, such linear terms will lead to a prefactor, $N{b}^{2}/l$, in the partition function, resulting in an additional term in the free energy of the form ${k}_{\rm{B}}T{\rm{ln}}l$ or an additional term in the force, ${k}_{\rm{B}}T/l$. From this argument it could be concluded that an independent non-Gaussian perturbation will contribute a topological charge to the force-extension curve. If there are two independent non-Gaussian perturbations, ${\Delta }x$ and ${\Delta }y$, integration of these two independent perturbations would result in a prefactor ${(N{b}^{2}/l)}^{2}$ and, therefore, two topological charges (see Fig. 4c). For different entangling modes, the topological charge number could be different and a simple way to determine the charge number is to count the number of independent non-Gaussian perturbations. Knots or self-entanglements inside the chain may also contribute to the topological charge number and unfortunately the above method cannot be extended to this type of dynamical topological constraints.

4Full-screen View

Physical origin of topological charges of polymer entanglements. (a) Gaussian Perturbation: When there is no pole, a small fluctuation ${\Delta }x$ will cause the chain length (in terms of the blob model) to increase about ${\Delta }{x}^{2}$. But this fluctuation can be eliminated by the Gaussian integral during the evaluation of partition function. (b) When one pole is presented, a small fluctuation ${\Delta }x$ in some section of the chain will cause the chain to elongate about ${\Delta }x$. This fluctuation cannot be adsorbed and will contribute a topological charge. (c) Two independent non-Gaussian perturbations contribute two topological charges. For the given entangling mode (two-pole), there are two possible independent fluctuating points which might cause the chain to extend about ${\Delta }x$ and ${\Delta }y$ (also see Fig. S6 in ESI), whose influences cannot be erased. Topological charges of different entangled modes of the two-pole case are given in Fig. S7 (in ESI).

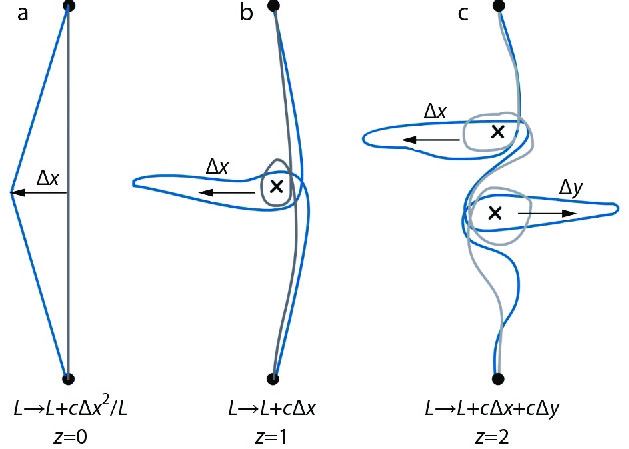
Although many important theoretical results have been obtained in the random walk on free groups^[9] as well as in the problem of a ring polymer in an array of obstacles,^[7,8] unfortunately, these results are difficult to be applied in the current work.

CONCLUSIONS

In summary, we have developed a superspace approach to studying the statistical mechanics of an ideal polymer chain entangled with n fixed poles. This approach gives a simpler solution to the one-pole problem compared with the solutions obtained by previous researchers.^[1−6] Furthermore, the superspace approach enables us to compute the force-extension curves of a polymer chain entangling with one pole or two poles. The results reveal that generically the force-extension curves contain two terms at large extension. The first term is linear in the effective extension, reflecting the entropic contribution to the free energy. Whereas the second term is proportional to the inverse of the effective extension, reflecting a topological contribution to the free energy. The topological term is determined by the topological charge number of the entangling mode. The origin of the topological charge is revealed by perturbing the blob model of the chain. Each independent non-Gaussian perturbation gives a topological charge. This topological term characterizes the intrinsic nature of polymer entanglements with the static topological constraints.