INTRODUCTION
Since the pioneering discovery of dendrimers due to Tomalia and coworkers,[1] dendritic polymers such as dendrimers and hyperbranched polymers have caused particular interest for their special structures and properties.[2−5] Compared with dendrimers, hyperbranched polymers have imperfect structures, but possess the features of relatively convenient synthesis and low cost,[4,5] and therefore can be easily industrialized. With the numerous relevant studies, some characteristic properties of hyperbranched polymers have been found such as low viscosity, high solubility, without entanglement, and with a large number of functional terminal groups. So far, hyperbranched polymers have been widely utilized in blending modification, surface modification, coating, catalytic reaction, and drug delivery.[6,7]
As is well known, there are two representative methods for preparing hyperbranched polymers. One is the polycondensation of 

Following these relevant experiments,[9−29] some theoretical investigations on SCVP systems have been well presented. In 1997, the SCVP system of pure inimers was investigated for the first time by Müller, Yan and Wulkow.[30,31] Subsequently, binary and ternary SCVP systems have been extensively studied by various methods.[32−49] Among these studies, much attention has been paid to the polymerization mechanism, kinetics, size distribution, average molecular weights, dispersity, degree of branching, mean-square radius of gyration, and so forth. These theoretical work has not only offered rich information to learn about various SCVP systems but also inspired some new research interest.
With the rapid developments in both theoretical and experimental studies on different SCVP systems, the semi-batch process (known also as the semi-continuous process) has attracted an increasing attention since it is closely related to large-scale applications of hyperbranched polymers in various fields.[50−58] It is well known that for a polymerization system, the procedure by which a polymerization is carried out can lead to a significant effect on the polymerization kinetics, dynamics and physical properties of resultant polymers. As far as this aspect is concerned, depending on the manner that the reactants are added into the reactor, polymerization processes can be classified into the batch, semi-batch, and continuous processes, respectively.
In a batch process, all the reactants are fed into the reactor at the beginning of a polymerization, and no material is added into or removed from the reactor during the polymerization. A semi-batch process refers to the case that reactants would be added into the reactor during the polymerization, while the products may also be removed from the reactor. In general, only a portion of reactants is initially loaded into the reactor, whereas the remainder would be fed according to a predetermined schedule. Unlike batch and semi-batch processes, a continuous process involves both a feeding of reactants and a removal of products such that there is usually a balance between the input and output streams.
In essence, these three types of feeding operations signify different local reaction conditions such as concentrations of individual species including monomers, initiators, and possible chain transfer agents. As such, polymers produced from the same reactants may possess quite different properties depending on the distinct feeding processes. It is therefore expected that there is an obvious effect of the feeding process on the final properties of polymers such as the average molecular weights, polydispersity, degree of branching and possible copolymer composition.
Experimentally, a batch process needs the modest demanding and the least amount of control, and hence it is mainly used for pure academic interest. A drawback in the batch process is that the drifts of molecular weight distribution and composition distribution are very common because reactant concentrations decrease gradually during the polymerization. In contrast to the batch process, a continuous process tends to be applied when a large volume of polymers is manufactured. In practice, most continuous processes are performed at a relatively steady reaction condition. In this way, the drift of molecular weight distribution can be well inhibited. However, it is inevitable that a high instrumentation cost and a long uninterrupted reaction time are usually involved. By comparison, in a semi-batch process, the corresponding drifts can be substantially reduced since the concentration of reactants can be controlled by an appropriate predetermined feeding schedule. Consequently, a polymerization can even be carried out under starved conditions to prepare polymers with desired properties.
In addition to the above-mentioned features, the versatility of the semi-batch mode is also closely related to the problem of exotherm. As is well known, some living polymerizations are so fast that the released heat due to polymerization becomes a potential hazard. However, controlling the feeding details in the semi-batch process allows a control over the reaction rate, and hence the exotherm. In other words, a low concentration of reactants can be maintained such that the semi-batch operation is compatible with the safety requirement. Moreover, the semi-batch process can also provide a regulation over the polymer structure and morphology for some polymerization systems.[50−58] In view of these obvious advantages, the semi-batch process has been widely utilized in both industry and academic interests.
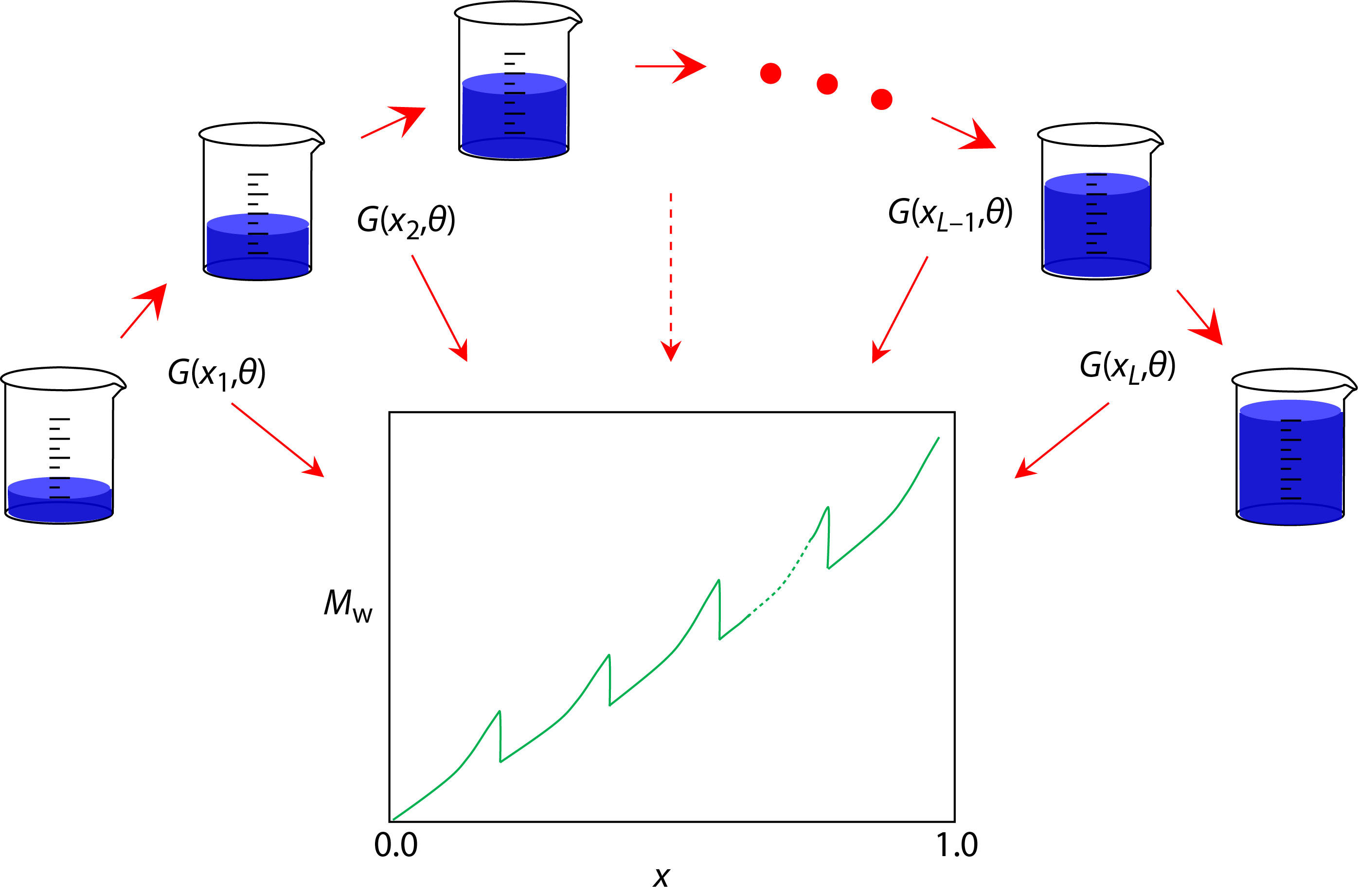
This work is motivated by the use of semi-batch process in the SCVP system consisting of pure inimers. An attempt is made to find how the semi-batch process regulates the average properties of hyperbranched polymers. This idea is based on the fact that a semi-batch process can always be decomposed into a series of time-sequenced feeding and polymerization steps. More importantly, the polymerization occurred between any two nearest neighbor steps is in essence equivalent to a batch process with various preexisted polymers formed by another SCVP system. Therefore, such a goal can be achieved once an average polymeric quantity associated with any two nearest neighbor steps is presented. This signifies that, if an average polymeric quantity for any two nearest neighbor polymerization steps is figured out, one is able to find the effect of the semi-batch process on the SCVP system.
For this purpose, our discussions will be firstly focused on the two nearest neighbor feedings, and then we generalize it to the whole feeding sequence. As usual, the number-, weight-, and z-average molecular weights denoted by 


This article is organized as follows. Firstly, an explicit generating function (GF) is proposed to calculate some average properties of the SCVP system with any initial distribution of preexisted polymers. Upon applying the GF method to the batch SCVP system of pure inimers, it reproduces identical results as given by previous studies, thereby validating the present GF method. Secondly, we generalized the present GF method to the semi-batch SCVP system, and investigated 


MODEL AND THEORY METHOD
Generating Function Method for an SCVP System with Any Initial Distribution of Polymers
As stated above, the effect of the semi-batch process on an SCVP system can be presented as long as the relationship of an averaged polymeric quantity associated with any two nearest neighbor feedings is obtained. In this section, a novel GF method will be proposed to achieve such a goal. Without loss of generality, we suppose that there have preexisted some polymers at the beginning of the SCVP system under consideration. This could correspond to two nearest neighbor polymerization steps, where the preexisted polymers come from either a previous polymerization step or a feeding operation, or from both them. In this way, an explicit GF will be employed to study such an SCVP system, which enables us to find how an average polymeric quantity depends on these preexisted polymers.
To proceed, we suppose that, for the present SCVP system, the number of preexisted polymers of 






Through successive reactions, molecules in the system can be linked together to form hyperbranched polymers of various sizes. As proposed by Müller, Yan and Wulkow, the evolution of the size distribution of polymers with time 

where 



Considering that the initial conversion of vinyl groups A has been arranged to be zero, then there would be 




where the number of active sites 

This is an explicit relationship between the conversion 


in which 
Note that there are 









Substituting 


In order to determine 


where 






It is obvious that through the initial conditions of the system, solving this equation will enable us to obtain 


The partial differential equation given by Eq. (8) is known as Burgers equation,[59,60] and the corresponding characteristics of 



where 












From the definition of the GF given in Eq. (7), the explicit expressions of 


The derivation of 





where 





Bear in mind that the mass of an inimer has been used as the unit mass, the number-, weight-, and z-average molecular weights, and Đ can be calculated from the derived 

For the system under study, as a consequence of Eqs. (11) and (12), we have

where 






Now a question that arises naturally is whether the present GF method is valid. To demonstrate its validity, the present GF method is applied to the batch SCVP system of pure inimers due to Müller, Yan and Wulkow.[30] Assume that there exist 





Making use of Eq. (11) and differentiating both sides of this equation with respect to 






Alternatively, these results can be directly derived by substituting 
More interestingly, 


where 




All the results presented in Eqs. (15) and (17) are identical with those obtained in the batch SCVP system,[30] thereby validating the present GF method. Furthermore, as a direct generalization, the present GF method will be employed to discuss the effect of the semi-batch process on the average polymeric quantities of hyperbranched polymers. This can be carried out by considering the semi-batch process as a series of multi-step processes of feeding and polymerization because any two nearest neighbour steps have been essentially solved by the present GF method.
A Unified Treatment on the Semi-batch SCVP System
For a polymerization system under the semi-batch mode, all the feeding operations are usually performed according to a predetermined schedule. Therefore the whole polymerization is exactly a multi-step process. This means that, at the beginning of each polymerization step, there are always some preexisted polymers resulting either from a previous polymerization or from the present feeding, or from both of them. As done in the previous section, these discrete steps can be further investigated one by one with the aid of the present GF method. Throughout the work, each feeding operation was considered to be instantaneous such that the response of the system during such an infinitesimal time interval can be neglected.
We assume that only inimers are initially loaded into the reactor, which is labeled as the zeroth feeding, for convenience. Subsequently, the first polymerization step begins until the conversion arrives at a predetermined conversion 

In this way, one can find that a polymerization and a feeding are always involved in each step. For clarity, a sequence of feedings and reactions in an SCVP system can be schematically illustrated in Fig. 1, where the semi-batch process was considered to be an 


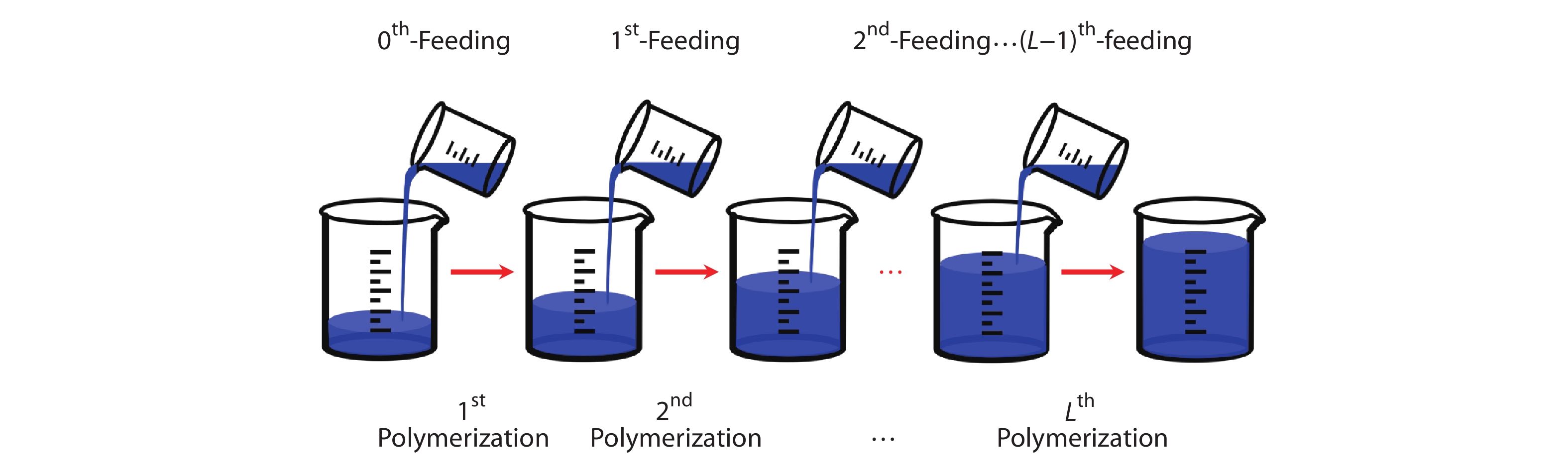
Now the semi-batch SCVP system would be investigated as an application of the present GF method, which enables us to treat the situation that allows polymers of various sizes to be added into the reactor in each feeding. From the results given in previous section, it has been found that these average polymeric quantities associated with two nearest neighbor steps are closely related to each other. As such, 


As schemed in Fig. 1, for any two nearest neighbor steps, for example, the 





Note that the 






where 






In analogy with Eqs. (9) and (10), the most important two equations resulting from the GF method can be found as:

where 






Making use of Eq. (19), the 



Likewise, 






where the quantity 

which denotes the ratio of the 


It should be stressed that the quantity 









RESULTS AND DISCUSSION
In this section, several average polymeric quantities for the semi-batch SCVP system would be calculated. Meanwhile, the MC simulation is also performed to verify the corresponding analytical results. It can be seen from Eq. (21), 




Case I: Feeding the same amount of inimers in each step
The first feeding way corresponds to the case that the number of fed inimers in each step keeps always the same as each other, which is widely employed in practice and would be referred to as the Case I. This simply means that the number of the fed inimers is equal to that loaded initially (the zero-th feeding in Fig. 1). More precisely, we have for 

where 

Clearly, feeding the same number of inimers in each step signifies that 


where 





In obtaining these, 

The above results manifest that the average properties of resultant polymers would be influenced by all the previous polymerization steps. They can be evaluated in a straightforward manner when the conversions of vinyl groups A and feeding details in each step are specified. Namely, for the Case I, one needs 



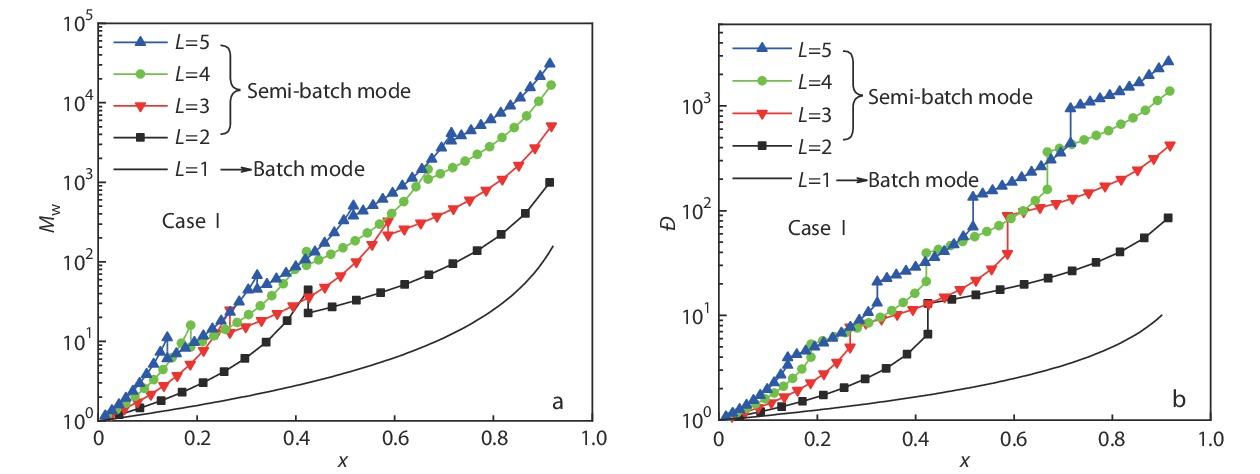
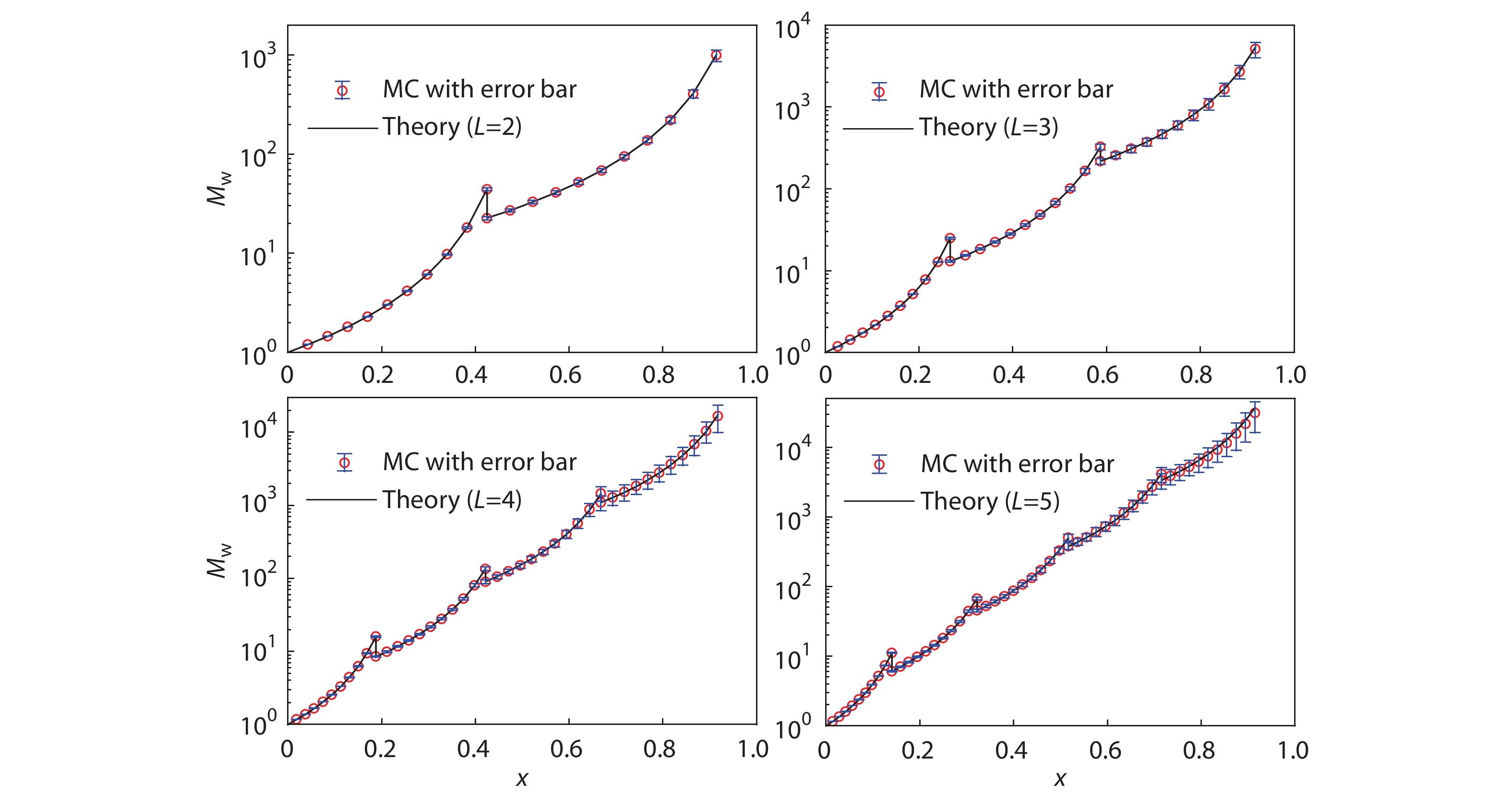
As an illustration, 






| Case I | Conversion |
 |  |
 |  |
 |  |
 |  |
Seen from Fig. 2, we can find the variations of 





Case II: Feeding inimers to maintain the same number of free vinyl groups in each step
The second case is that feeding inimers is to maintain a fixed initial concentration of free vinyl groups A, which is referred to as the Case II. This kind of feeding implies that the consumption fraction of vinyl groups would be supplied by the feeding operation. In other words, the number of vinyl groups at the beginning of each polymerization step always remains a constant. In a sense, this indicates a steady rate for a polymerization, i.e.:

where 



Given that the number of inimers at the initial stage is 


in which we have arranged 



In obtaining these equations, we have used the results 

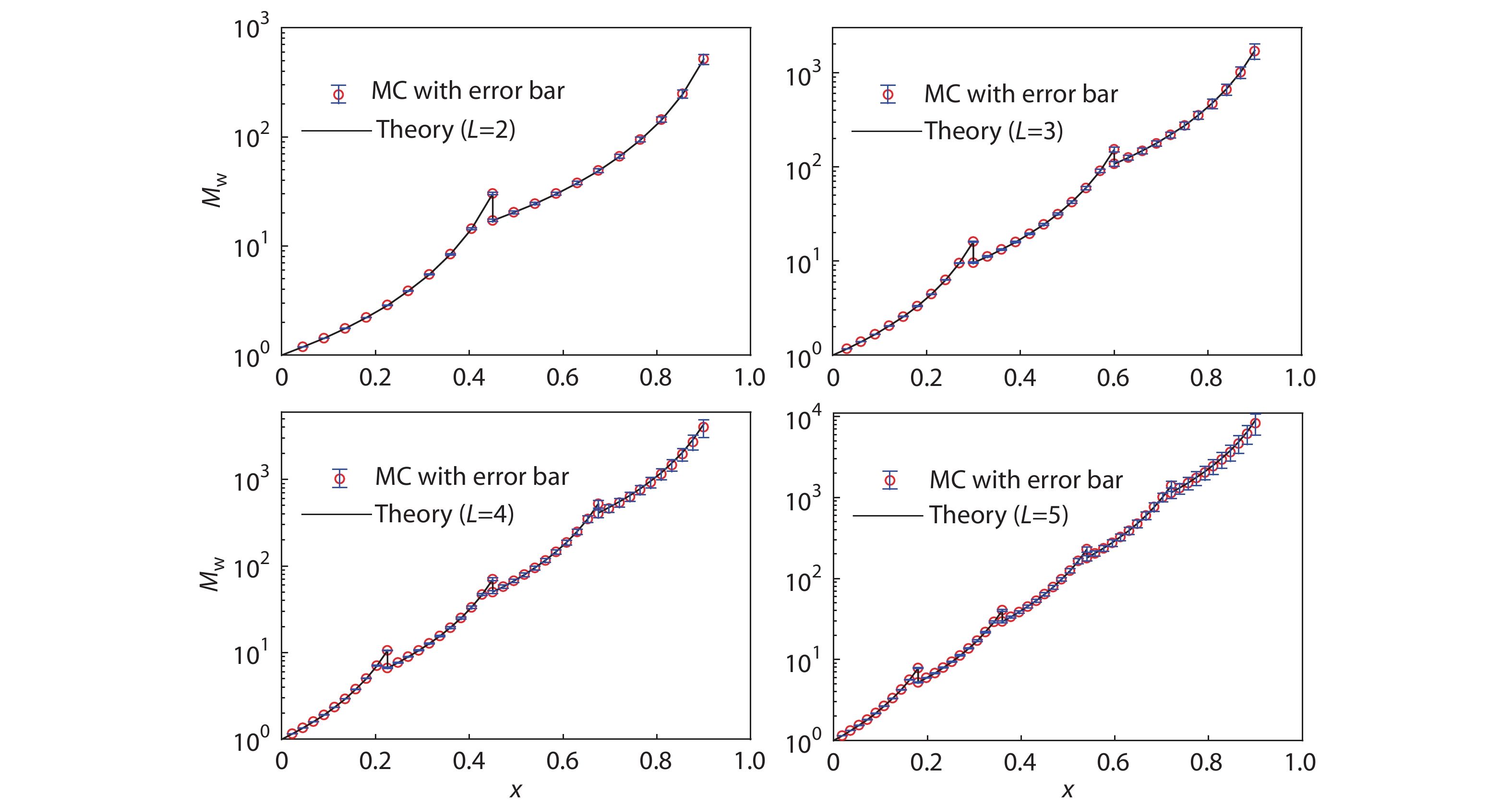
Through Eq. (28), 




| Case II | Conversion |
 |  |
 |  |
 |  |
 |  |


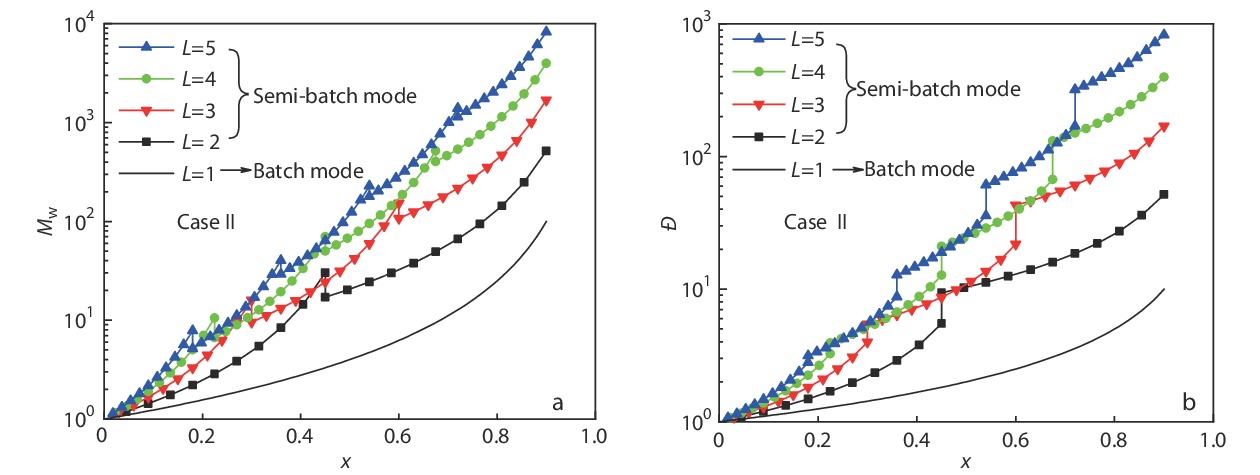
Compared with that in the batch mode, 

Note that for the present semi-batch SCVP system, the problem of exotherm could be solved because of its characteristic operation of multiple feedings. In practice, depending on the specific reaction conditions, various species and fed amount can be well designed to control the polymerization. In so doing, the semi-batch mode becomes compatible with the safe requirement. This is, of course, particularly important for applying SCVP method to prepare hyperbranched polymers in industry and chemical engineering.
Monte Carlo Simulation for a Semi-batch SCVP System
In this section, MC simulations on the semi-batch SCVP system would be performed for the case that only inimers are fed into the reactor. In particular, the simulation results for Cases I and II discussed in this work would be compared with the corresponding analytical results. For a stochastic chemical reaction, a set of master equations can be constructed on the basis of the reaction mechanism.[63,64] In the present SCVP system, the change in size distribution of polymers is subject to the differential kinetic equations given in Eq. (1). Therefore the evolution of MC simulation would be governed by the corresponding master equation. For easy of presentation, here we only outline how to use MC method to simulate a semi-batch SCVP system.
Assume that the system consists of treelike molecules with size distribution 






According to the Eqs. (1) and (2), if 



where the term with Kronecker symbol 







This indicates that 



The simulation can be performed by a simple sampling over all reaction events because of the identity of 



To test the program, we have firstly implemented 100 simulations on the batch SCVP system, where the number of inimers in each was fixed as N=105. As a consequence of the simulation, 














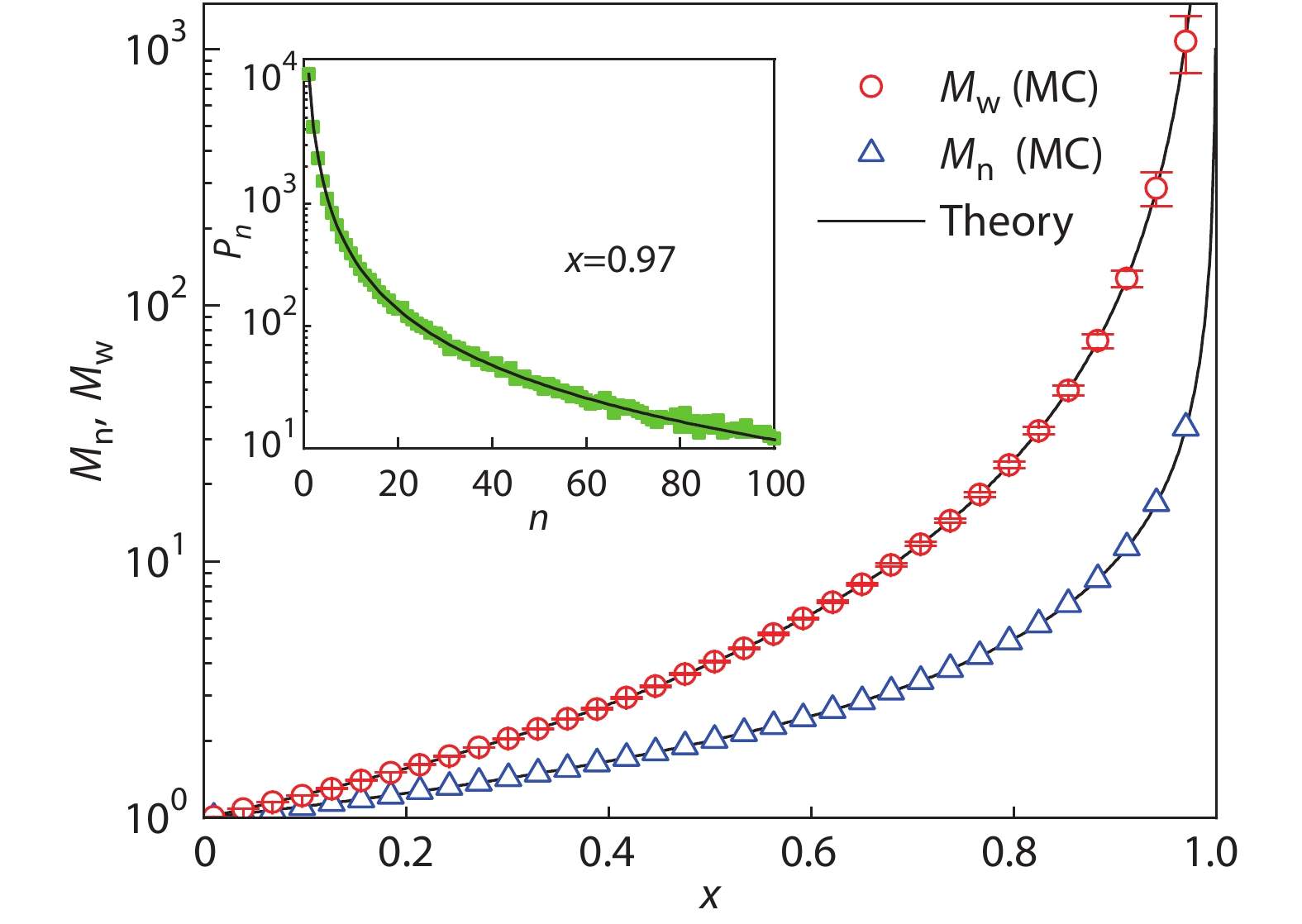
Clearly, the key quantity obtained from the MC simulation is the number distribution of hyperbranched polymers, and hence the molecular weight distribution (MWD). This is measurable in experiments. Interestingly, the variation of MWD with time can be directly carried out provided that the reaction rate 



An excellent agreement between the theoretical and simulation results can be observed. At a fixed 



The above simulation results manifested that the present GF method can be employed to evaluate 




CONCLUSIONS
In summary, we presented a GF method for investigating the SCVP system under the semi-batch mode by treating it as an 



Clearly, given the predetermined schedule that contains the number of batches 
Although the removal of various polymers from the reactor is not yet considered in this work, it is not difficult to generalize the GF method to take into account such operations. This can be realized by adding the corresponding terms in Eqs. (18) and (22) by specifying the degree of polymerization and amount of those removed polymers in each step. Therefore, the effect of the removal operation on the SCVP system can be found.
Note that the present semi-batch SCVP system was treated as an 
Dendritic macromolecules: synthesis of starburst dendrimers
Macromolecules 1986 19 2466 2468Tomalia, D. A.; Baker, H.; Dewald, J.; Hall, M.; Kallos, G.; Martin, S.; Roeck, J.; Ryder, J.; Smith, P. Dendritic macromolecules: synthesis of starburst dendrimers. Macromolecules 1986, 19, 2466−2468.
Water soluble hyperbranched polyphenylene: “a unimolecular micelle?”
J. Am. Chem. Soc. 1990 112 4592 4593Kim, Y. H.; Webster, O. W. Water soluble hyperbranched polyphenylene: “a unimolecular micelle?” J. Am. Chem. Soc. 1990, 112, 4592−4593.
Self-condensing vinyl polymerization: an approach to dendritic materials
Science 1995 269 1080 1083Fréchet, J. M. J.; Henmi, M.; Gitsov, I.; Aoshima, S.; Leduc, M. R.; Grubbs, R. B. Self-condensing vinyl polymerization: an approach to dendritic materials. Science 1995, 269, 1080−1083.
Hyperbranched polymers: from synthesis to applications
Prog. Polym. Sci. 2004 29 183 275Gao, C.; Yan, D. Y. Hyperbranched polymers: from synthesis to applications. Prog. Polym. Sci. 2004, 29, 183−275.
Hyperbranched and highly branched polymer architectures-synthetic strategies and major characterization aspects
Chem. Rev. 2009 109 5924 5973Voit, B. I.; Lederer, A. Hyperbranched and highly branched polymer architectures-synthetic strategies and major characterization aspects. Chem. Rev. 2009, 109, 5924−5973.
Hyperbranched polymers: advances from synthesis to applications
Chem. Soc. Rev. 2015 44 4091 4130Zheng, Y. C.; Li, S. P.; Weng, Z. L.; Gao, C. Hyperbranched polymers: advances from synthesis to applications. Chem. Soc. Rev. 2015, 44, 4091−4130.
Molecular size distribution in three dimensional polymers. VI. Branched polymers containing A-R-Bf-1 type units
J. Am. Chem. Soc. 1952 74 2718 2723Flory, P. J. Molecular size distribution in three dimensional polymers. VI. Branched polymers containing A-R-Bf-1 type units. J. Am. Chem. Soc. 1952, 74, 2718−2723.
Preparation of hyperbranched polyacrylates by atom transfer radical polymerization. 1. Acrylic AB* monomers in “living” radical polymerizations
Macromolecules 1997 30 5192 5194Matyjaszewski, K.; Gaynor, S. G.; Kulfan, A.; Podwika, M. Preparation of hyperbranched polyacrylates by atom transfer radical polymerization. 1. Acrylic AB* monomers in “living” radical polymerizations. Macromolecules 1997, 30, 5192−5194.
Preparation of hyperbranched polyacrylates by atom transfer radical polymerization. 2. Kinetics and mechanism of chain growth for the self-condensing vinyl polymerization of 2-((2-bromopropionyl)oxy)ethyl acrylate
Macromolecules 1997 30 7034 7041Matyjaszewski, K.; Gaynor, S. G.; Müller, A. H. E. Preparation of hyperbranched polyacrylates by atom transfer radical polymerization. 2. Kinetics and mechanism of chain growth for the self-condensing vinyl polymerization of 2-((2-bromopropionyl)oxy)ethyl acrylate. Macromolecules 1997, 30, 7034−7041.
Hyperbranched methacrylates by self-condensing group transfer polymerization
Macromol. Rapid Commun. 1997 18 865 873Simon, P. F. W.; Radke, W.; Müller, A. H. E. Hyperbranched methacrylates by self-condensing group transfer polymerization. Macromol. Rapid Commun. 1997, 18, 865−873.
Kinetic investigation of self-condensing group transfer polymerization
Macromolecules 2004 37 7548 7558Simon, P. F. W.; Müller, A. H. E. Kinetic investigation of self-condensing group transfer polymerization. Macromolecules 2004, 37, 7548−7558.
Controlling polymer topology by atom transfer radical self-condensing vinyl polymerization of p-(2-bromoisobutyloylmethyl)styrene
Macromolecules 2010 43 8790 8798Dong, B. T.; Dong, Y. Q.; Du, F. S.; Li, Z. C. Controlling polymer topology by atom transfer radical self-condensing vinyl polymerization of p-(2-bromoisobutyloylmethyl)styrene. Macromolecules 2010, 43, 8790−8798.
Synthesis of hyperbranched polyacrylates by a chloroinimer approach
Macromolecules 2010 43 5222 5232Pugh, C.; Singh, A.; Samuel, R.; Bernal Ramos, K. M. Synthesis of hyperbranched polyacrylates by a chloroinimer approach. Macromolecules 2010, 43, 5222−5232.
Synthesis of hyperbranched and highly branched methacrylates by self-condensing group transfer copolymerization
Macromolecules 2001 34 6206 6213Simon, P. F. W.; Müller, A. H. E. Synthesis of hyperbranched and highly branched methacrylates by self-condensing group transfer copolymerization. Macromolecules 2001, 34, 6206−6213.
Synthesis and characterization of hyperbranched polyacrylates in the presence of a tetrafunctional initiator with higher reactivity than monomer by self-condensing vinyl polymerization
Polymer 2001 42 6733 6740Hong, C. Y.; Pan, C. Y.; Huang, Y.; Xu, Z. D. Synthesis and characterization of hyperbranched polyacrylates in the presence of a tetrafunctional initiator with higher reactivity than monomer by self-condensing vinyl polymerization. Polymer 2001, 42, 6733−6740.
Synthesis and characterization of hyperbranched polyacrylates in the presence of a tetrafunctional initiator with higher reactivity than monomer by self-condensing vinyl polymerization
Polymer 2001 42 9385 9391Hong, C. Y.; Pan, C. Y. Synthesis and characterization of hyperbranched polyacrylates in the presence of a tetrafunctional initiator with higher reactivity than monomer by self-condensing vinyl polymerization. Polymer 2001, 42, 9385−9391.
New approaches to hyperbranched poly(4-chloromethylstyrene) and introduction of various functional end groups by polymer-analogous reactions
J. Polym. Sci., Part A: Polym. Chem. 2010 48 2224 2235Georgi, U.; Erber, M.; Stadermann, J.; Abulikemu, M.; Komber, H.; Lederer, A.; Voit, B. New approaches to hyperbranched poly(4-chloromethylstyrene) and introduction of various functional end groups by polymer-analogous reactions. J. Polym. Sci., Part A: Polym. Chem. 2010, 48, 2224−2235.
Synthesis of structurally controlled hyperbranched polymers using a monomer having hierarchical reactivity
Nat. Commun. 2017 8 1863Lu, Y.; Nemoto, T.; Tosaka, M.; Yamago, S. Synthesis of structurally controlled hyperbranched polymers using a monomer having hierarchical reactivity. Nat. Commun. 2017, 8, 1863.
Synthesis and characterization of branched polyelectrolytes. Preparation of hyperbranched poly(acrylic acid) via self-condensing atom transfer radical copolymerization
Macromolecules 2002 35 9270 9281Mori, H.; Seng, D. C.; Lechner, H.; Zhang, M.; Müller, A. H. E. Synthesis and characterization of branched polyelectrolytes. Preparation of hyperbranched poly(acrylic acid) via self-condensing atom transfer radical copolymerization. Macromolecules 2002, 35, 9270−9281.
Synthesis of highly branched cationic polyelectrolytes via self-condensing atom transfer radical copolymerization with 2-(diethylamino)ethyl methacrylate
Macromolecules 2004 37 2054 2066Mori, H.; Walther, A.; André, X.; Lanzendörfer, M. G.; Müller, A. H. E. Synthesis of highly branched cationic polyelectrolytes via self-condensing atom transfer radical copolymerization with 2-(diethylamino)ethyl methacrylate. Macromolecules 2004, 37, 2054−2066.
Synthesis of hyperbranched glycopolymers via self-condensing atom transfer radical copolymerization of a sugar-carrying acrylate
Macromolecules 2005 38 9 18Muthukrishnan, S.; Jutz, G.; Andre, X.; Mori, H.; Müller, A. H. E. Synthesis of hyperbranched glycopolymers via self-condensing atom transfer radical copolymerization of a sugar-carrying acrylate. Macromolecules 2005, 38, 9−18.
Synthesis and characterization of methacrylate-type hyperbranched glycopolymers via self-condensing atom transfer radical copolymerization
Macromolecules 2005 38 3108 3119Muthukrishnan, S.; Mori, H.; Müller, A. H. E. Synthesis and characterization of methacrylate-type hyperbranched glycopolymers via self-condensing atom transfer radical copolymerization. Macromolecules 2005, 38, 3108−3119.
Preparation of branched polyacrylonitrile through self-condensing vinyl copolymerization
J. Appl. Polym. Sci. 2008 110 494 500Liu, Q.; Xiong, M.; Cao, M.; Chen, Y. Preparation of branched polyacrylonitrile through self-condensing vinyl copolymerization. J. Appl. Polym. Sci. 2008, 110, 494−500.
Hyperbranched polymers by type II photoinitiated self-condensing vinyl polymerization
Macromol. Rapid Commun. 2016 37 650 654Aydogan, C.; Ciftci, M.; Yagci, Y. Hyperbranched polymers by type II photoinitiated self-condensing vinyl polymerization. Macromol. Rapid Commun. 2016, 37, 650−654.
Synthesis and characterization of surface-grafted hyperbranched glycomethacrylates
Macromolecules 2006 39 2743 2750Muthukrishnan, S.; Erhard, D. P.; Mori, H.; Müller, A. H. E. Synthesis and characterization of surface-grafted hyperbranched glycomethacrylates. Macromolecules 2006, 39, 2743−2750.
Self-condensing reversible complexation-mediated copolymerization for highly branched polymers with in situ formed inimers
Polym. Chem. 2017 8 6844 6852Yang, H.; Wang, Z.; Cao, L.; Huang, W.; Jiang, Q.; Xue, X.; Song, Y.; Jiang, B. Self-condensing reversible complexation-mediated copolymerization for highly branched polymers with in situ formed inimers. Polym. Chem. 2017, 8, 6844−6852.
Hyperbranced polymers by photoinduced self-condensing vinyl polymerization using bisbenzodioxinone
Macromol. Chem. Phys. 2017 218 1700045Aydogan, C.; Ciftci, M.; Kumbaraci, V.; Talinli, N.; Yagci, Y. Hyperbranced polymers by photoinduced self-condensing vinyl polymerization using bisbenzodioxinone. Macromol. Chem. Phys. 2017, 218, 1700045.
Hyperbranched polymers via RAFT self-condensing vinyl polymerization
Polym. Chem. 2016 7 3361 3369Alfurhood, J. A.; Bachler, P. R.; Sumerlin, B. S. Hyperbranched polymers via RAFT self-condensing vinyl polymerization. Polym. Chem. 2016, 7, 3361−3369.
Molecular parameters of hyperbranched polymers made by self-condensing vinyl polymerization. 1. Molecular weight distribution
Macromolecules 1997 30 7015 7023Müller, A. H. E.; Yan, D. Y.; Wulkow, M. Molecular parameters of hyperbranched polymers made by self-condensing vinyl polymerization. 1. Molecular weight distribution. Macromolecules 1997, 30, 7015−7023.
Molecular parameters of hyperbranched polymers made by self-condensing vinyl polymerization. 2. Degree of branching
Macromolecules 1997 30 7024 7033Yan, D. Y.; Müller, A. H. E.; Matyjaszewski, K. Molecular parameters of hyperbranched polymers made by self-condensing vinyl polymerization. 2. Degree of branching. Macromolecules 1997, 30, 7024−7033.
Effect of core-forming molecules on molecular weight distribution and degree of branching in the synthesis of hyperbranched polymers
Macromolecules 1998 31 239 248Radke, W.; Litvinenko, G.; Müller, A. H. E. Effect of core-forming molecules on molecular weight distribution and degree of branching in the synthesis of hyperbranched polymers. Macromolecules 1998, 31, 239−248.
Molecular weight distribution of hyperbranched polymers generated by self-condensing vinyl polymerization in presence of a multifunctional initiator
Macromolecules 1999 32 245 250Yan, D. Y.; Zhou, Z. P.; Müller, A. H. E. Molecular weight distribution of hyperbranched polymers generated by self-condensing vinyl polymerization in presence of a multifunctional initiator. Macromolecules 1999, 32, 245−250.
Molecular parameters of hyperbranched copolymers obtained by self-condensing vinyl copolymerization. 1. Equal rate constants
Macromolecules 1999 32 2410 2419Litvinenko, G. I.; Simon, P. F. W.; Müller, A. H. E. Molecular parameters of hyperbranched copolymers obtained by self-condensing vinyl copolymerization. 1. Equal rate constants. Macromolecules 1999, 32, 2410−2419.
Molecular parameters of hyperbranched copolymers obtained by self-condensing vinyl copolymerization. 2. Non-equal rate constants
Macromolecules 2001 34 2418 2426Litvinenko, G. I.; Simon, P. F. W.; Müller, A. H. E. Molecular parameters of hyperbranched copolymers obtained by self-condensing vinyl copolymerization. 2. Non-equal rate constants. Macromolecules 2001, 34, 2418−2426.
Molecular weight averages and degree of branching in self-condensing vinyl copolymerization in the presence of multifunctional initiators
Macromolecules 2002 35 4577 4583Litvinenko, G. I.; Müller, A. H. E. Molecular weight averages and degree of branching in self-condensing vinyl copolymerization in the presence of multifunctional initiators. Macromolecules 2002, 35, 4577−4583.
Kinetic model of hyperbranched polymers formed by self-condensing vinyl polymerization of AB* monomers in the presence of multifunctional core molecules with different reactivities
Polymer 2003 44 877 882Cheng, K. C. Kinetic model of hyperbranched polymers formed by self-condensing vinyl polymerization of AB* monomers in the presence of multifunctional core molecules with different reactivities. Polymer 2003, 44, 877−882.
Monte Carlo simulation of hyperbranched copolymerizations in the presence of a multifunctional initiator
Macromol. Theor. Simul. 2001 10 196 203He, X. H.; Liang, H. J.; Pan, C. Y. Monte Carlo simulation of hyperbranched copolymerizations in the presence of a multifunctional initiator. Macromol. Theor. Simul. 2001, 10, 196−203.
Self-condensing vinyl polymerization in the presence of a multifunctional initiator with unequal rate constant: Monte Carlo simulation
Polymer 2003 44 6697 6706He, X. H.; Liang, H. J.; Pan, C. Y. Self-condensing vinyl polymerization in the presence of a multifunctional initiator with unequal rate constant: Monte Carlo simulation. Polymer 2003, 44, 6697−6706.
A general model for the kinetics of self-condensing vinyl polymerization
Macromolecules 2008 41 4429 4434Zhou, Z. P.; Yan, D. Y. A general model for the kinetics of self-condensing vinyl polymerization. Macromolecules 2008, 41, 4429−4434.
Effect of multifunctional initiator on self-condensing vinyl polymerization with nonequal molar ratio of stimulus to monomer
Macromolecules 2009 42 4047 4052Zhou, Z. P.; Yan, D. Y. Effect of multifunctional initiator on self-condensing vinyl polymerization with nonequal molar ratio of stimulus to monomer. Macromolecules 2009, 42, 4047−4052.
A statistical theory for self-condensing vinyl polymerization
J. Chem. Phys. 2009 131 074101Zhao, Z. F.; Wang, H. J.; Ba, X. W. A statistical theory for self-condensing vinyl polymerization. J. Chem. Phys. 2009, 131, 074101.
Statistical properties for the self-condensing vinyl polymerization in presence of multifunctional core initiators
Polymer 2011 52 854 865Zhao, Z. F.; Wang, H. J.; Ba, X. W. Statistical properties for the self-condensing vinyl polymerization in presence of multifunctional core initiators. Polymer 2011, 52, 854−865.
Kinetic analysis of self-condensing vinyl polymerization with unequal reactivities
Chin. Sci. Bull. 2008 53 3516 3521Zhou, Z. P.; Wang, G. J.; Yan, D. Y. Kinetic analysis of self-condensing vinyl polymerization with unequal reactivities. Chin. Sci. Bull. 2008, 53, 3516−3521.
The radius of gyration for a ternary self-condensing vinyl polymerization system
Sci. China Chem. 2015 58 1875 1863Hong, X. Z.; Zhao, Z. F.; Wang, H. J.; Ba, X. W. The radius of gyration for a ternary self-condensing vinyl polymerization system. Sci. China Chem. 2015, 58, 1875−1863.
Markovian approach to self-condensing vinyl polymerization: distributions of molecular weights, degrees of branching, and molecular dimensions
Macromol. Theor. Simul. 2015 24 117 132Tobita, H. Markovian approach to self-condensing vinyl polymerization: distributions of molecular weights, degrees of branching, and molecular dimensions. Macromol. Theor. Simul. 2015, 24, 117−132.
Hyperbranched polymers formed through self-condensing vinyl polymerization in a continuous stirred-tank reactor: 1. Molecular weight distribution
Macromol. Theor. Simul. 2018 27 1800027Tobita, H. Hyperbranched polymers formed through self-condensing vinyl polymerization in a continuous stirred-tank reactor: 1. Molecular weight distribution. Macromol. Theor. Simul. 2018, 27, 1800027.
Hyperbranched polymers formed through self-condensing vinyl polymerization in a continuous stirred-tank reactor: 2. Branched architecture
Macromol. Theor. Simul. 2018 27 1800028Tobita, H. Hyperbranched polymers formed through self-condensing vinyl polymerization in a continuous stirred-tank reactor: 2. Branched architecture. Macromol. Theor. Simul. 2018, 27, 1800028.
Detailed structural analysis of the hyperbranched polymers formed in self-condensing vinyl polymerization
Macromol. Theor. Simul. 2019 28 1800061Tobita, H. Detailed structural analysis of the hyperbranched polymers formed in self-condensing vinyl polymerization. Macromol. Theor. Simul. 2019, 28, 1800061.
Effect of feed rate on structure of hyperbranched polymers formed by stepwise addition of AB2 monomers into multifunctional cores
Polymer 2003 44 1259 1266Cheng, K. C. Effect of feed rate on structure of hyperbranched polymers formed by stepwise addition of AB2 monomers into multifunctional cores. Polymer 2003, 44, 1259−1266.
Effect of feed rate on structure of hyperbranched polymers formed by self-condensing vinyl polymerization in semibatch reactor
Macromolecules 2005 38 8252 8257Cheng, K. C.; Chuang, T. H.; Chang, J. S.; Guo, W. J.; Su, W. F. Effect of feed rate on structure of hyperbranched polymers formed by self-condensing vinyl polymerization in semibatch reactor. Macromolecules 2005, 38, 8252−8257.
Design and control of copolymer composition distribution in living radical polymerization using semi-batch feeding policies: a model simulation
Macromol. Theor. Simul. 2006 15 356Wang, R.; Luo, Y. W.; Li, B. G.; Sun, X. Y.; Zhu, S. P. Design and control of copolymer composition distribution in living radical polymerization using semi-batch feeding policies: a model simulation. Macromol. Theor. Simul. 2006, 15, 356.
Synthesis and characterization of hyperbranched polyacrylamide using semibatch reversible addition-fragmentation chain transfer (RAFT) polymerization
Macromolecules 2010 43 40624069Wang, W. J.; Wang, D. M.; Li, B. G.; Zhu S. P. Synthesis and characterization of hyperbranched polyacrylamide using semibatch reversible addition-fragmentation chain transfer (RAFT) polymerization. Macromolecules 2010, 43, 40624069.
Kinetics and modeling of semi-batch RAFT copolymerization with hyperbranching
Macromolecules 2012 45 28 38Wang, D. M.; Li, X. H.; Wang, W. J.; Gong, X.; Li, B. G.; Zhu, S. P. Kinetics and modeling of semi-batch RAFT copolymerization with hyperbranching. Macromolecules 2012, 45, 28−38.
Semibatch RAFT polymerization for branched polyacrylamide production: effect of divinyl monomer feeding policies
AICHE J. 2013 59 1322 1333Wang, D. M.; Wang, W. J.; Li, B. G.; Zhu, S. P. Semibatch RAFT polymerization for branched polyacrylamide production: effect of divinyl monomer feeding policies. AICHE J. 2013, 59, 1322−1333.
Effect of feed rate of monofunctional monomers on structure of hyperbranched copolymers formed by self-condensing vinyl copolymerization in semibatch reactor
Eur. Polym. J. 2014 60 98 105Cheng, K. C. Effect of feed rate of monofunctional monomers on structure of hyperbranched copolymers formed by self-condensing vinyl copolymerization in semibatch reactor. Eur. Polym. J. 2014, 60, 98−105.
Improved control through a semi-batch process in RAFT-mediated polymerization utilizing relatively poor leaving groups
Polym. Chem. 2015 6 7945 7948Ilchev, A.; Pfukwa, R.; Hlalele, L.; Smit, M.; Klumperman, B. Improved control through a semi-batch process in RAFT-mediated polymerization utilizing relatively poor leaving groups. Polym. Chem. 2015, 6, 7945−7948.
Effect of feed rate of end-capping molecules on structure of hyperbranched polymers formed from monomers A2 and B4 in semibatch process
Eur. Polym. J. 2017 89 339 348Cheng, K. C.; Lai, W. J. Effect of feed rate of end-capping molecules on structure of hyperbranched polymers formed from monomers A2 and B4 in semibatch process. Eur. Polym. J. 2017, 89, 339−348.
Stochastic simulation of chemical kinetics
Annu. Rev. Phys. Chem. 2007 58 35 55Gillespie, D. T. Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 2007, 58, 35−55.