INTRODUCTION
Flow- or strain-induced crystallization (FIC or SIC) of polymers occurs not only in processing like film blowing, injection molding and fiber spinning, but also in service of some polymers like natural rubber and shape memory materials.[1-5] Though large efforts from both academic and industrial communities have been devoted for understanding FIC, it still remains as a classic and important challenge in polymer physics.[5,6] In recent two decades, new techniques such as in situ synchrotron radiation X-ray scattering and computer simulations provide more in-depth information about the kinetic pathway of FIC, but we still lack a thermodynamic theory of FIC to incorporate these new observations, such as the mesophase or precursor, shish-kebab, and the emergence of new crystal forms.[7-15]
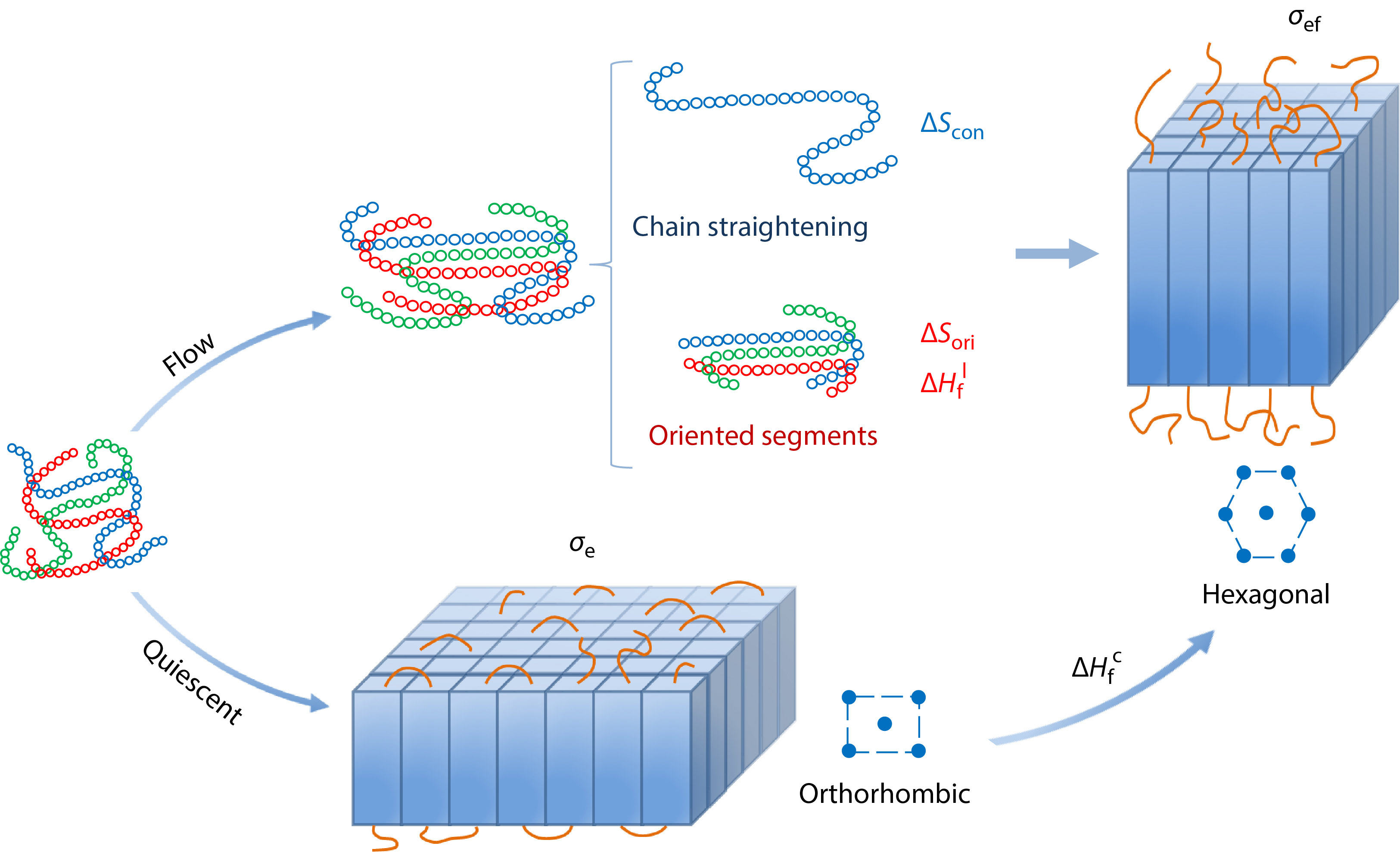
At present, Flory’s conformational entropy reduction model (CERM) proposed in 1947 is the most widely recognized model for FIC, which was originated from uniaxial stretching of natural rubber.[16] CERM depicts a process of flow-induced chain straightening, which results in conformational entropy reduction (CER, 






where 




where 



Conformational entropy is a global parameter on the individual chains, while nucleation and crystallization are packing processes involving local multi-chain segments, suggesting that 














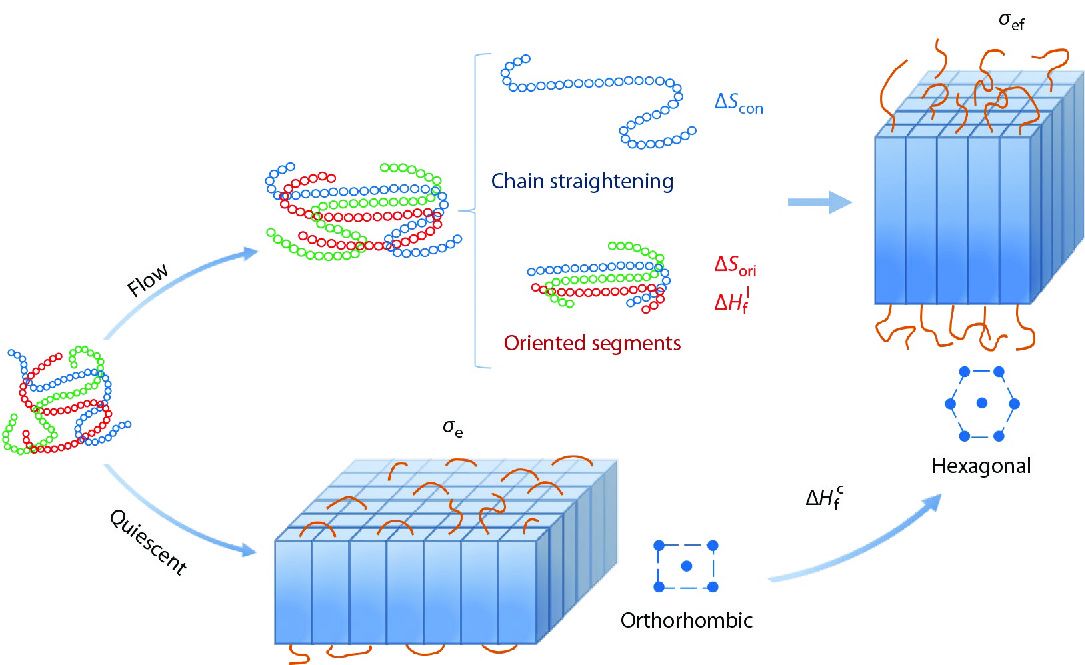
Based on the experiment and simulation results, FIC models incorporating the effects of orientation, chain interaction, new crystal morphology and structure have been proposed in recent years, which, however, were considered separately. Chen et al.[20] introduced the orientation entropy and the chain interaction between the ordered segments, while Liu et al.[24] took the free energy change of the final crystalline state into account and proposed the entropy reduction-energy change (ER-EC) model. Although these efforts make a stepwise progress for understanding FIC, a unified FIC theory incorporating the above three factors has not been developed yet.
In this work, starting from classic nucleation theory, we propose a thermodynamic model for FIC to unify flow-induced changes of conformational entropy 







THEORY AND METHOD
To deduce the uFIC model, we first incorporate flow-induced variations of entropy and enthalpy into the chemical potential 

where 






Then, Eq. (3) can be written as

where 


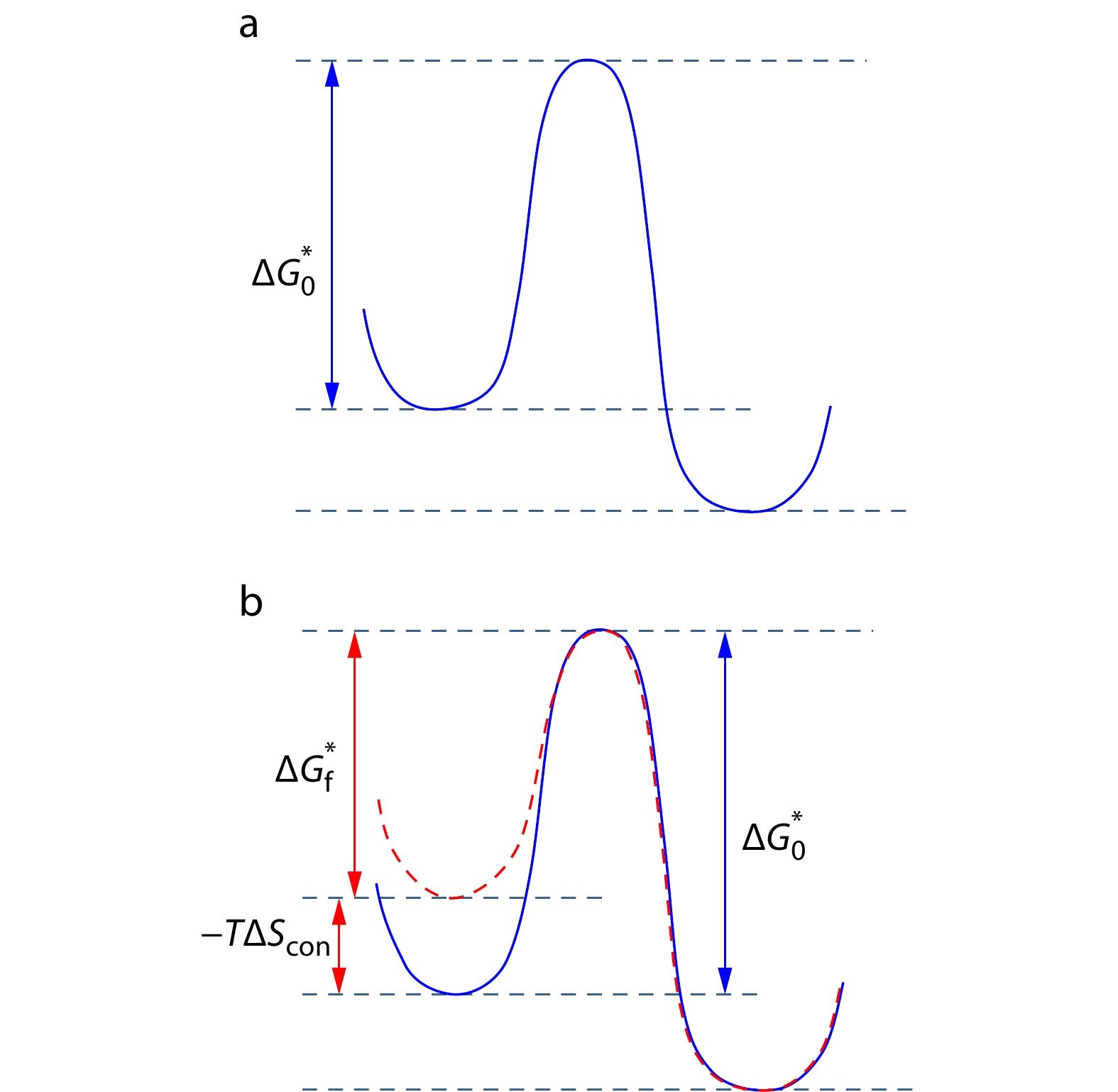
The CERM and other FIC models generally assume that the free energies of the critical nucleus and the final state under flow keep the same as those at quiescent condition. However, at the same crystallization temperature 




where 










where we assume that the ratios of these two values to the length 




Substituting these expressions of 


Inserting 


where 


where 


DISCUSSION
As the uFIC model takes both flow-induced modifications of liquid and crystal into account, it is expected that this model can explain all the experimental observations of FIC. To analyze how flow affects nucleation process, we compare the nucleation barriers at flow and quiescent conditions. Here we assume the free energy density of the crystal side surface under flow is unchanged, 

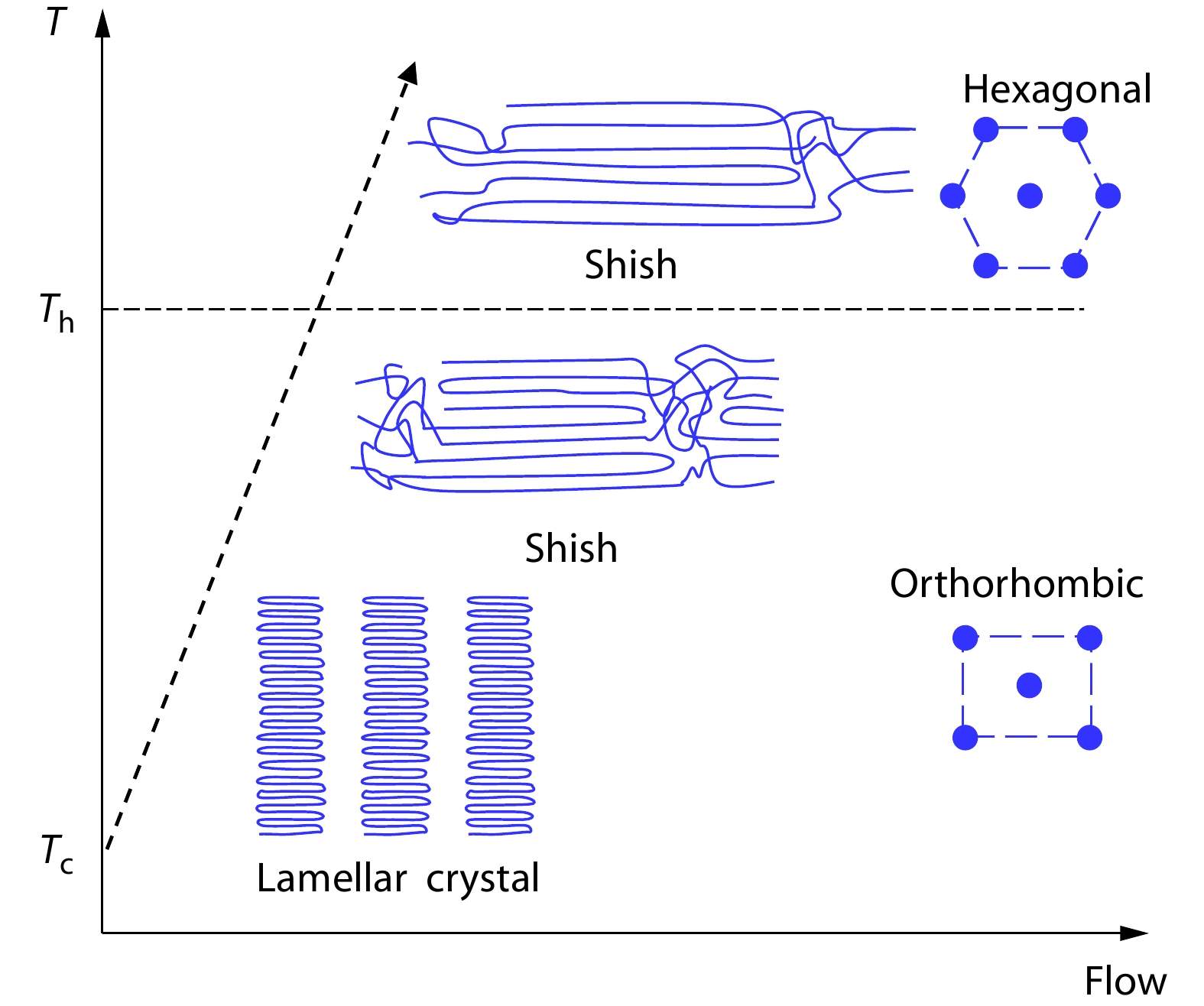
Taking the nucleation barrier expressed in Eq. (14) as the basic starting point, we are going to discuss the 4 characteristic observations in FIC experiments: (i) accelerating nucleation; (ii) changing the nucleus from lamellae to shish; (iii) preordering; and (iv) inducing new crystal form.
(i) Accelerating Nucleation
If we assume flow only changes the melt entropy, Eq. (14) can be re-written as

Below the equilibrium melting temperature (














(ii) Changing the Nucleus from Lamellae to Shish
Considering that the free energy density of the crystal end surface increases due to the external flow, 



Here, combined with Eq. (3), we clarify the determinants of the critical crystal nucleus size, including conformational entropy change 






Taking a lamellar nucleus with 








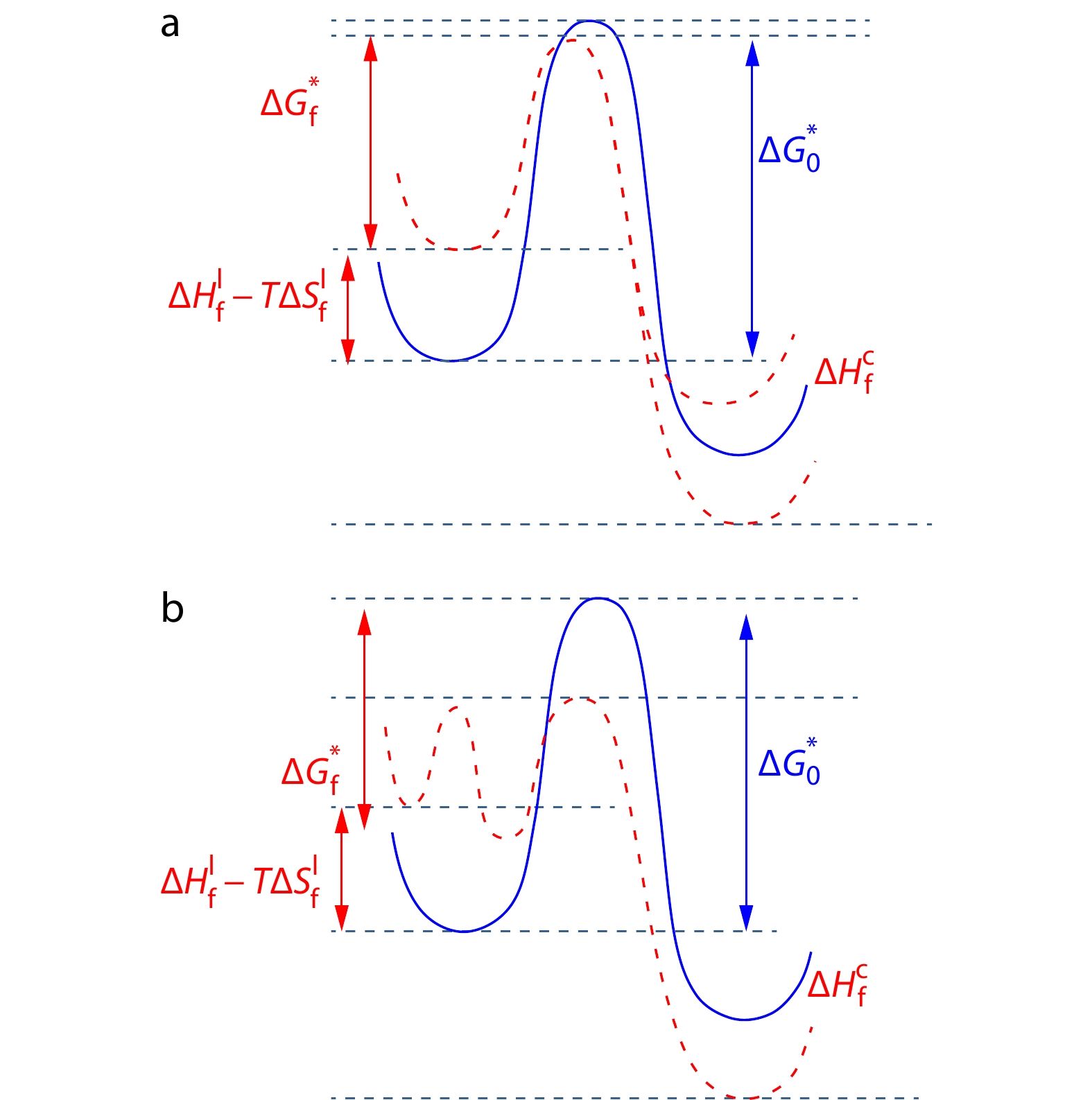
(iii) Preordering
If a precursor emerges in FIC with no change of the final crystal form, which may be either a transient kinetic state or a thermodynamic metastable phase corresponding to a free energy local minimum, the ratio of nucleation barriers is

Obviously, when FIC occurs, 






(iv) Inducing New Crystal Form
Finally we consider the situation with the competition between two crystal forms like flow-induced orthorhombic and hexagonal phases of PE, where 

where 


















The above discussion is qualitative and based on some reasonable assumptions, which, however, demonstrates the capability of the uFIC model on understanding experimental observations. The CERM may be numerically applied to fit the flow accelerated nucleation rate, but experimental result suggests 




CONCLUSIONS
Taking all the changes of chain conformation, chain orientation, interaction of ordered segments in the initial polymer melt, and the final crystal morphology and structure into account, we propose a uFIC model and rewrite the expression of nucleation free energy barrier under flow, as presented in Eq. (13). Our model can not only effectively explain the flow-accelerated polymer nucleation, but also offer understandings of other FIC experimental observations. It theoretically verifies that the intermediate phase or precursor is a metastable phase only when the free energy density of the interface between the preordering and the melt is smaller than that of the crystal-melt interface. Based on the nucleation barrier under flow, the competition of different crystal forms in the flow can be clarified. Taking PE as an example, the critical transition temperature between orthorhombic and hexagonal crystal forms can be determined by comparing the crystallization enthalpy and the end surface free energy density. In conclusion, our model has the potential to be applied to explain all the observations of FIC experiments which have been done before and can provide a theoretical guidance for further FIC study.
APPENDIX
The estimation of 


where 









Considering the influence of orientation on the free energy of the initial melt, the parallel arrangement of the local stretched segments leads to the reduction in the number of possible conformations of the molecular chain, which is considered as the entropy effect. At the same time, there is an interaction between the parallel oriented segments, which manifests as an influence on enthalpy.[20] The entropy change of the melt caused by the oriented segments is defined as the orientation entropy, based on statistical mechanics and Maier-Saupe theory,[47] which can be expressed as

where 









Through Taylor expansion, ignoring higher-order terms, according to the Eqs. (20) and (21), the contribution of orientation to the free energy of the melt can be written as follows

where a, b, and c are constants related to pressure and temperature.
The existence of crystals with different morphologies and structures under flow indicates that the existence of the enthalpy change of the crystal 
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Processing pathways decide polymer properties at the molecular level
Macromolecules 2019 52 7146 7156Chandran, S.; Baschnagel, J.; Cangialosi, D.; Fukao, K.; Glynos, E.; Janssen, L. M. C.; Müller, M.; Muthukumar, M.; Steiner, U.; Xu, J.; Napolitano, S.; Reiter, G. Processing pathways decide polymer properties at the molecular level. Macromolecules 2019, 52, 7146−7156.
Multiscale and multistep ordering of flow-induced nucleation of polymers
Chem. Rev. 2018 118 1840 1886Cui, K.; Ma, Z.; Tian, N.; Su, F.; Liu, D.; Li, L. Multiscale and multistep ordering of flow-induced nucleation of polymers. Chem. Rev. 2018, 118, 1840−1886.
Shape-memory polymers
Angew. Chem. Int. Ed. 2002 41 2034 2057Lendlein, A.; Kelch, S. Shape-memory polymers. Angew. Chem. Int. Ed. 2002, 41, 2034−2057.
Flow-induced crystallization of polymers: molecular and thermodynamic considerations
Macromolecules 2016 49 1505 1517Wang, Z.; Ma, Z.; Li, L. Flow-induced crystallization of polymers: molecular and thermodynamic considerations. Macromolecules 2016, 49, 1505−1517.
The tough journey of polymer crystallization: battling with chain flexibility and connectivity
Macromolecules 2019 52 3575 3591Tang, X.; Chen, W.; Li, L. The tough journey of polymer crystallization: battling with chain flexibility and connectivity. Macromolecules 2019, 52, 3575−3591.
Understanding flow-induced crystallization in polymers: a perspective on the role of molecular simulations
J. Rheol. 2019 63 203 214Graham, R. S. Understanding flow-induced crystallization in polymers: a perspective on the role of molecular simulations. J. Rheol. 2019, 63, 203−214.
Nonequilibrium nature of flow-induced nucleation in isotactic polypropylene
Macromolecules 2015 48 694 699Cui, K.; Liu, D.; Ji, Y.; Huang, N.; Ma, Z.; Wang, Z.; Lv, F.; Yang, H.; Li, L. Nonequilibrium nature of flow-induced nucleation in isotactic polypropylene. Macromolecules 2015, 48, 694−699.
Langevin dynamics simulations of early stage shish-kebab crystallization of polymers in extensional flow
J. Chem. Phys. 2003 118 6648 6655Dukovski, I.; Muthukumar, M. Langevin dynamics simulations of early stage shish-kebab crystallization of polymers in extensional flow. J. Chem. Phys. 2003, 118, 6648−6655.
Correlation between flow-induced nucleation morphologies and strain in polyethylene: from uncorrelated oriented point-nuclei, scaffold-network, and microshish to shish
Macromolecules 2013 46 3435 3443Liu, D.; Tian, N.; Cui, K.; Zhou, W.; Li, X.; Li, L. Correlation between flow-induced nucleation morphologies and strain in polyethylene: from uncorrelated oriented point-nuclei, scaffold-network, and microshish to shish. Macromolecules 2013, 46, 3435−3443.
Molecular simulation of flow-enhanced nucleation in n-eicosane melts under steady shear and uniaxial extension
J. Chem. Phys. 2016 145 244903Nicholson, D. A.; Rutledge, G. C. Molecular simulation of flow-enhanced nucleation in n-eicosane melts under steady shear and uniaxial extension. J. Chem. Phys. 2016, 145, 244903.
Molecular dynamics simulation of stretch-induced crystallization in polyethylene: emergence of fiber structure and molecular network
Macromolecules 2019 52 1695 1706Yamamoto, T. Molecular dynamics simulation of stretch-induced crystallization in polyethylene: emergence of fiber structure and molecular network. Macromolecules 2019, 52, 1695−1706.
Flow-induced density fluctuation assisted nucleation in polyethylene
J. Chem. Phys. 2018 149 224901Tang, X.; Yang, J.; Tian, F.; Xu, T.; Xie, C.; Chen, W.; Li, L. Flow-induced density fluctuation assisted nucleation in polyethylene. J. Chem. Phys. 2018, 149, 224901.
Stretch-induced coil–helix transition in isotactic polypropylene: a molecular dynamics simulation
Macromolecules 2018 51 3994 4002Xie, C.; Tang, X.; Yang, J.; Xu, T.; Tian, F.; Li, L. Stretch-induced coil–helix transition in isotactic polypropylene: a molecular dynamics simulation. Macromolecules 2018, 51, 3994−4002.
Inducing uniform single-crystal like orientation in natural rubber with constrained uniaxial stretch
Soft Matter 2015 11 5044 5052Zhou, W.; Meng, L.; Lu, J.; Wang, Z.; Zhang, W.; Huang, N.; Chen, L.; Li, L. Inducing uniform single-crystal like orientation in natural rubber with constrained uniaxial stretch. Soft Matter 2015, 11, 5044−5052.
Shish-kebab crystallites initiated by shear fracture in bulk polymers
Macromolecules 2018 51 480 487Nie, Y.; Zhao, Y.; Matsuba, G.; Hu, W. Shish-kebab crystallites initiated by shear fracture in bulk polymers. Macromolecules 2018, 51, 480−487.
Thermodynamics of crystallization in high polymers. I. Crystallization induced by stretching
J. Chem. Phys. 1947 15 397 408Flory, P. J. Thermodynamics of crystallization in high polymers. I. Crystallization induced by stretching. J. Chem. Phys. 1947, 15, 397−408.
A continuum model for flow-induced crystallization of polymer melts
J. Rheol. 1999 43 85 109Doufas, A. K.; Dairanieh, I. S.; McHugh, A. J. A continuum model for flow-induced crystallization of polymer melts. J. Rheol. 1999, 43, 85−109.
Microrheological modeling of flow-induced crystallization
Macromolecules 2001 34 5030 5036Coppola, S.; Grizzuti, N.; Maffettone, P. L. Microrheological modeling of flow-induced crystallization. Macromolecules 2001, 34, 5030−5036.
PolySTRAND model of flow-induced nucleation in polymers
Phys. Rev. Lett. 2020 124 147802Read, D. J.; McIlroy, C.; Das, C.; Harlen, O. G.; Graham, R. S. PolySTRAND model of flow-induced nucleation in polymers. Phys. Rev. Lett. 2020, 124, 147802.
Frustrating strain-induced crystallization of natural rubber with biaxial stretch
ACS Appl. Mater. Interfaces 2019 11 47535 47544Chen, X.; Meng, L.; Zhang, W.; Ye, K.; Xie, C.; Wang, D.; Chen, W.; Nan, M.; Wang, S.; Li, L. Frustrating strain-induced crystallization of natural rubber with biaxial stretch. ACS Appl. Mater. Interfaces 2019, 11, 47535−47544.
An assessment of models for flow-enhanced nucleation in an n-alkane melt by molecular simulation
J. Rheo. 2019 63 465Nicholson, D. A.; Rutledge, G. C. An assessment of models for flow-enhanced nucleation in an n-alkane melt by molecular simulation. J. Rheo. 2019, 63, 465.
Effect of flow-induced nematic order on polyethylene crystal nucleation
Macromolecules 2020 53 7650 7657Zhang, W.; Larson, R. G. Effect of flow-induced nematic order on polyethylene crystal nucleation. Macromolecules 2020, 53, 7650−7657.
The non-equilibrium phase diagrams of flow-induced crystallization and melting of polyethylene
Sci. Rep. 2016 6 32968Wang, Z.; Ju, J.; Yang, J.; Ma, Z.; Liu, D.; Cui, K.; Yang, H.; Chang, J.; Huang, N.; Li, L. The non-equilibrium phase diagrams of flow-induced crystallization and melting of polyethylene. Sci. Rep. 2016, 6, 32968.
Extension-induced nucleation under near-equilibrium conditions: the mechanism on the transition from point nucleus to shish
Macromolecules 2014 47 6813 6823Liu, D.; Tian, N.; Huang, N.; Cui, K.; Wang, Z.; Hu, T.; Yang, H.; Li, X.; Li, L. Extension-induced nucleation under near-equilibrium conditions: the mechanism on the transition from point nucleus to shish. Macromolecules 2014, 47, 6813−6823.
Crystallization and dissolution of flow-induced precursors
Phys. Rev. Lett. 2008 100 048302Balzano, L.; Kukalyekar, N.; Rastogi, S.; Peters, G. W.; Chadwick, J. C. Crystallization and dissolution of flow-induced precursors. Phys. Rev. Lett. 2008, 100, 048302.
Self-acceleration of nucleation and formation of shish in extension-induced crystallization with strain beyond fracture
Macromolecules 2012 45 5477 5486Cui, K.; Meng, L.; Tian, N.; Zhou, W.; Liu, Y.; Wang, Z.; He, J.; Li, L. Self-acceleration of nucleation and formation of shish in extension-induced crystallization with strain beyond fracture. Macromolecules 2012, 45, 5477−5486.
High-strength polyethylene fibres from solution and gel spinning
J. Mater. Sci. 1985 20 2281 2302Barham, P. J.; Keller, A. High-strength polyethylene fibres from solution and gel spinning. J. Mater. Sci. 1985, 20, 2281−2302.
Kinetic process of shish formation: from stretched network to stabilized nuclei
Macromolecules 2015 48 5276 5285Cui, K.; Ma, Z.; Wang, Z.; Ji, Y.; Liu, D.; Huang, N.; Chen, L.; Zhang, W.; Li, L. Kinetic process of shish formation: from stretched network to stabilized nuclei. Macromolecules 2015, 48, 5276−5285.
Simulation of shish-kebab crystallite induced by a single prealigned macromolecule
Macromolecules 2002 35 7172 7174Hu, W.; Frenkel, D.; Mathot, V. Simulation of shish-kebab crystallite induced by a single prealigned macromolecule. Macromolecules 2002, 35, 7172−7174.
Hierarchic structure of shish-kebab by neutron scattering in a wide Q range
Macromolecules 2007 40 3650 3654Kanaya, T.; Matsuba, G.; Ogino, Y.; Nishida, K.; Shimizu, H. M.; Shinohara, T.; Oku, T.; Suzuki, J.; Otomo, T. Hierarchic structure of shish-kebab by neutron scattering in a wide Q range. Macromolecules 2007, 40, 3650−3654.
Dissolution and re-emergence of flow-induced shish in polyethylene with a broad molecular weight distribution
Macromolecules 2016 49 2724 2730Ma, Z.; Balzano, L.; Peters, G. W. M. Dissolution and re-emergence of flow-induced shish in polyethylene with a broad molecular weight distribution. Macromolecules 2016, 49, 2724−2730.
Fractionation of polymers by crystallization from solution, III. On the morphology of fibrillar polyethylene crystals grown in solution
Kolloid-Zeitschrift und Zeitschrift für Polymere 1965 205 160 162Pennings, A. J.; Kiel, A. M. Fractionation of polymers by crystallization from solution, III. On the morphology of fibrillar polyethylene crystals grown in solution. Kolloid-Zeitschrift und Zeitschrift für Polymere 1965, 205, 160−162.
Hydrodynamically induced crystallization of polymers from solution
Colloid Polym. Sci. 1977 255 532 542Pennings, A. J.; Lageveen, R.; de Vries, R. S. Hydrodynamically induced crystallization of polymers from solution. Colloid Polym. Sci. 1977, 255, 532−542.
Nucleation in polymer crystallization
Adv. Chem. Phys. 2003 128 1 63Muthukumar, M. Nucleation in polymer crystallization. Adv. Chem. Phys. 2003, 128, 1−63.
Coarse-grained simulations of flow-induced nucleation in semicrystalline polymers
Phys. Rev. Lett. 2009 103 115702Graham, R. S.; Olmsted, P. D. Coarse-grained simulations of flow-induced nucleation in semicrystalline polymers. Phys. Rev. Lett. 2009, 103, 115702.
Strain-induced crystallization during relaxation following biaxial stretching of PET films: a real-time mechano-optical study
Macromolecules 2015 48 4657 4668Hassan, M. K.; Cakmak, M. Strain-induced crystallization during relaxation following biaxial stretching of PET films: a real-time mechano-optical study. Macromolecules 2015, 48, 4657−4668.
Transition from chain- to crystal-network in extension induced crystallization of isotactic polypropylene
J. Chem. Phys. 2017 146 014901Wang, Z.; Su, F.; Ji, Y.; Yang, H.; Tian, N.; Chang, J.; Li, L. Transition from chain- to crystal-network in extension induced crystallization of isotactic polypropylene. J. Chem. Phys. 2017, 146, 014901.
Competition of crystal nucleation to fabricate the oriented semi-crystalline polymers
Polymer 2013 54 3402 3407Nie, Y.; Gao, H.; Yu, M.; Hu, Z.; Reiter, G.; Hu, W. Competition of crystal nucleation to fabricate the oriented semi-crystalline polymers. Polymer 2013, 54, 3402−3407.
Polymer crystal–melt interfaces and nucleation in polyethylene
Soft Matter 2011 7 2909 2917Milner, S. T. Polymer crystal–melt interfaces and nucleation in polyethylene. Soft Matter 2011, 7, 2909−2917.
Crystallization and precursors during fast short-term shear
Macromolecules 2009 42 2088 2092Balzano, L.; Rastogi, S.; Peters, G. W. M. Crystallization and precursors during fast short-term shear. Macromolecules 2009, 42, 2088−2092.
An approach to the formation and growth of new phases with application to polymer crystallization: effect of finite size, metastability, and Ostwald's rule of stages
J. Mater. Sci. 1994 29 2579 2604Keller, A.; Hikosaka, M.; Rastogi, S.; Toda, A.; Barham, P. J.; Goldbeck-Wood, G. An approach to the formation and growth of new phases with application to polymer crystallization: effect of finite size, metastability, and Ostwald's rule of stages. J. Mater. Sci. 1994, 29, 2579−2604.
Melting and heat capacity of gel-spun, ultra-high molar mass polyethylene fibers
Polymer 2000 41 6237 6249Kwon, Y. K.; Boller, A.; Pyda, M.; Wunderlich, B. Melting and heat capacity of gel-spun, ultra-high molar mass polyethylene fibers. Polymer 2000, 41, 6237−6249.
Chain mobility in polymer systems: on the borderline between solid and melt. 2. Crystal size influence in phase transition and sintering of ultrahigh molecular weight polyethylene via the mobile hexagonal phase
Macromolecules 1998 31 5022 5031Rastogi, S.; Kurelec, L.; Lemstra, P. J. Chain mobility in polymer systems: on the borderline between solid and melt. 2. Crystal size influence in phase transition and sintering of ultrahigh molecular weight polyethylene via the mobile hexagonal phase. Macromolecules 1998, 31, 5022−5031.
Diffraction study of crystallite orientation in a stretched polychloroprene vulcanizate
J. Polym. Sci., Part A: Genr. Papers 1964 2 4391 4414Krigbaum, W. R.; Roe, R. J. Diffraction study of crystallite orientation in a stretched polychloroprene vulcanizate. J. Polym. Sci., Part A: Genr. Papers 1964, 2, 4391−4414.
Strain-induced crystallization, Part III: Theory
Polym. Eng. Sci. 1979 19 395 400Yeh, G. S. Y.; Hong, K. Z. Strain-induced crystallization, Part III: Theory. Polym. Eng. Sci. 1979, 19, 395−400.
Strain-induced crystallization, Part IV: Induction time analysis
Polym. Eng. Sci. 1979 19 401 405Yeh, G. S. Y.; Hong, K. Z.; Krueger, D. L. Strain-induced crystallization, Part IV: Induction time analysis. Polym. Eng. Sci. 1979, 19, 401−405.
Eine einfache molekular-statistische Theorie der nematischen kristallinflüssigen Phase. Teil II
Zeitschrift Naturforschung Teil A 1959 14 882Maier, W.; Saupe, A. Eine einfache molekular-statistische Theorie der nematischen kristallinflüssigen Phase. Teil II. Zeitschrift Naturforschung Teil A 1959, 14, 882.